Quick Sort
정렬방법
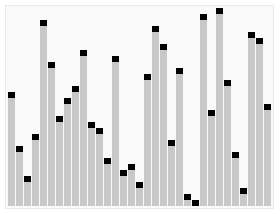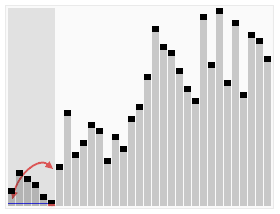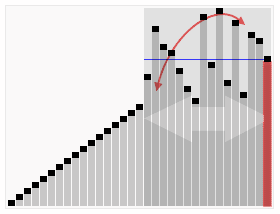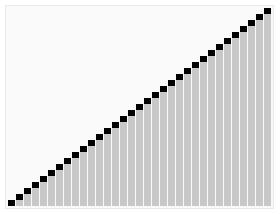출처:wikipedia
Quick sorting은 이전의 Merge sorting과 마찬가지로 divide and conquer 방식을 사용한다.
Pivot을 선택하여 pivot보다 작은값들은 왼쪽, 큰값들은 오른쪽으로 나눈 후 pivot을 제외하고(이 때 pivot은 이미 있어야 할 자리에 정렬되어있음.) 두개의 sub array로 나눠서 같은 작업을 분할 반복한다.
이 때 pivot을 선택하는 방법은 여러가지가 있다.
- 제일 첫번째를 pivot으로 선정
- 제일마지막을 pivot으로선정
- 가운데값을 pivot으로 선정
- random하게 pivot으로 선정
- 기타 등등..
이처럼 여러가지 방법 있으나, 무조건 첫번째나 제일 마지막을 선정하는 방법은 이미 정렬된 array에 대해서 아주 안좋은(O(n^2)) 성능을 보여준다. 따라서 랜덤하게 선정하거나 몇개의 랜덤값중 중간값을 선정하는 등 최적화를 한다.
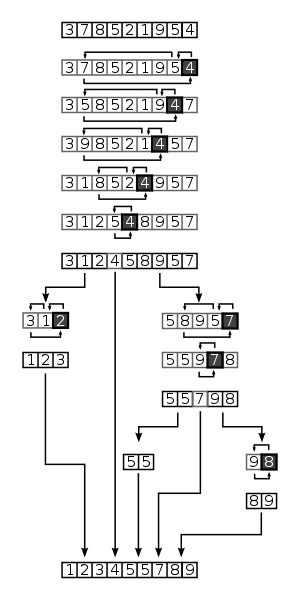last pivot exmaple. 출처: wikipedia
Time compelxity
- Worst case: 일반적으로 제일 큰 수나 작은 수의 원소를 pivot으로 선정했을 때, array가 이미 정렬되어 있으면 worst case의 time complexity를 가진다. 순환 호출에서 n번, 각 호출 안에서 비교연산 n번 -> O(n^2)
- best case: 일반적으로 항상 중간값을 pivot으로 선정할 때 best case의 time complexity를 가진다. 순환호출에서 2진트리를 나눠지는 경우 O(logn), 각 호출 안에서 비교연산 n번 -> O(nlogn)
Implementation
간단한 c++ 구현 예제
#include <stdio.h>
#include <iostream>
using namespace std;
int arr[11] = { 15,3,643,25,1,23,4,9,124,58, 55 };
int sorted_arr[11];
void swap(int &a, int &b)
{
int t = a;
a = b;
b = t;
}
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = low - 1; //i = pivot보다 작은 값의 최우측 위치
for (int j = low; j < high; j++) {
if (arr[j] < pivot)
swap(arr[++i], arr[j]);
}
swap(arr[i + 1], arr[high]); // i+1은 현재 피봇의 위치(자신보다 작은값의 오른쪽에 들어가야함)
return i + 1;
}
void quick_sort(int arr[], int low, int high)
{
int pivot;
if (low < high) {
pivot = partition(arr, low, high);
quick_sort(arr, low, pivot - 1);
quick_sort(arr, pivot + 1, high);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
quick_sort(arr,0,10);
for(int i=0; i<11; i++)
cout << arr[i] << "\n";
return 0;
}정리
- Quick sorting은 O(n)의 추가적인 공간이 필요한 Merge sorting과는 다르게 제자리 정렬이 가능하다. 즉 In-place sorting alogirthm이다.
- Quick sort는 Merge Sort보다 locality의 관점에서 더욱 효율적이다. locoality란 cpu가 cache나 메모리의 특정한 집중된 부분을 반복적으로 접근하는 것을 말한다. 운영체제의 pagination 특성 상 이 locality는 속도에 있어 상당한 도움을 받을 수 있다.
- 위의 이유 때문에 일반적으로 quick sort가 merge sort보다 빠르다. 하지만 데이터가 매우 크고 외부 저장소에 저장되있거나, merge sort를 linked list등으로 구현할 경우에는 더 좋은 성능을 발휘하기도 한다.
아래는 Merge sort와 Quick sort의 데이터 탐색 범위를 시각적으로 표현한 animation이다.
자세한 내용은 이미지의 출처 링크를 들어가면 읽을 수 있다.
- Merge sort
- Quick sort
