Introduction
Sorting Algorithm 시리즈에서는 여러가지 sorting 방법에 대해서 배운다. 데이터 구조를 배우면서 처음으로 배우는 algorithm 혹은 algorithm이라고 부르기 애매한(?) 그만큼 필수적이고 보편적인 지식이라고 할 수 있다.
이번 글은 대표적인 Sorting Algorithm 중에서도 단순간단하지만 Time complexity가 큰 selection,insertion,bubble sort에 대해서 다룬다. 간단하게 구현이 가능하고 어려운 개념이 없기 때문에 하나의 글에 정리하였다.
Bubble sort
정렬방법

출처:wikipedia
위의 애니메이션은 Bubble sort를 실행할 때 value (y축)가 index (x축)에 저장되어가는 모습을 시각적으로 나타낸 것이다. 이 모습이 마치 거품이 수면위로 떠오르는 것과 같다하여 Bubble sort 라는 이름이 붙었다고 한다.
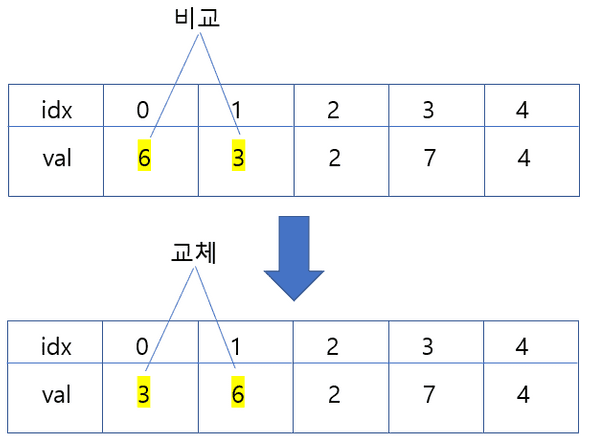
- Bubble sort의 기본적인 정렬 방법은 자신의 옆의 수와 비교를하고, 더 큰 수를 오른쪽에 위치시키는 것이다.
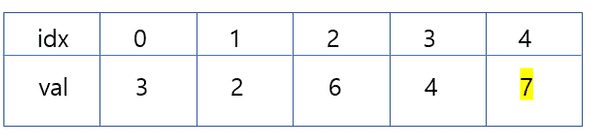
- 여기서 중요한 점은, 이렇게 비교를하다가 한바퀴를 다 돌면 배열의 제일 큰 수가 제일 마지막에 위치하게 된다는 점이다.
- 그렇다면 다음 회차에 비교할 때는, n-1번째랑 n번째를 비교를 할 필요가 없게된다. 즉, 회차마다 제일 마지막 인덱스를 하나씩 줄여가면서 비교를 하면 된다.
Time complexity
위의 방법대로 시행한다면 비교 횟수는 (n-1)+(n-2)+ ... +2+1 = n(n-1) * 1/2 이 된다.
이때 원소를 swap하는 횟수는
- best case(이미 정렬)의 경우 swap이 일어나지 않고
- worst case(역순 배치)의 경우 비교마다 swap이 일어나므로 마찬가지로 n(n-1) * 1/2이 될것이다.
따라서 normal bubble sort algorithm이라면 Avg Time complexity는 O(n^2)이 된다.
best case의 경우 성능을 improve하기
- 만약 best case(이미 정렬)의 경우 swap 여부의 flag 변수를 하나 설정한다.
- 비교 과정 중 한번이라도 swap이 일어났으면 flag를 true로 바꾸고, 아니라면 false로 유지한다.
- 첫번째 회차를 마치고 flag가 false라면 더이상의 진행을 끝내고 n-1의 횟수만에, 즉 O(n)만에 비교를 끝낼 수 있다.
Implementation
간단한 C++ 구현 예시
#include <stdio.h>
#include <iostream>
using namespace std;
int arr[10] = { 15,3,643,25,1,23,4,9,124,58 };
void swap(int &a, int &b) {
int temp;
temp = a;
a = b;
b = temp;
}
void bubble_sort(int arr[],int size) {
for (int i = size - 1; i > 0; i--) {
for (int j = 0; j <i; j++) {
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
bubble_sort(arr, 10);
for(int i=0; i<10; i++)
cout << arr[i] << "\n";
return 0;
}정리
구현이 쉽고 복잡한 로직이 없으나 기본적으로 매우 느리기 때문에 거의 사용하지 않는다.
Insertion sort
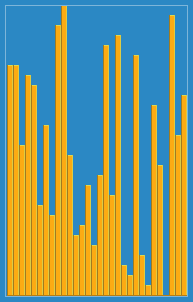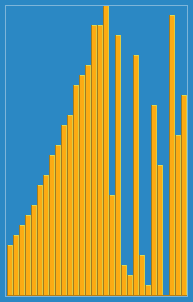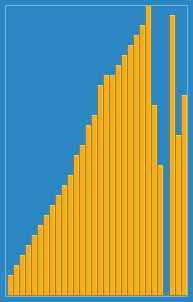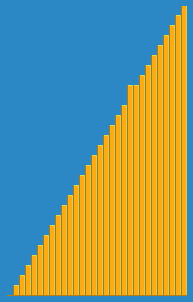
출처:wikipedia
정렬방법
- Insertion sort는 기본적으로 자신의 앞에있는 모든 수와 비교를 하면서 자신보다 크면 오른쪽으로 옮기고, 작으면 자신이 그자리에 들어가는 방법으로 정렬을 한다.
- 앞서 말했듯이 자신의 앞과 비교를 해야하기 때문에 2번째 수부터 비교대상(pivot)으로 선정한다.
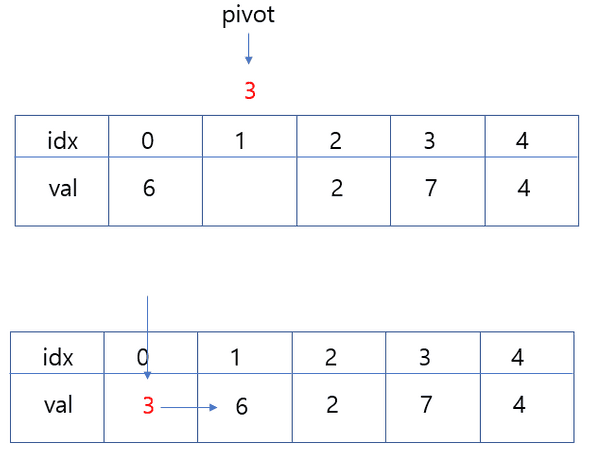
- 위와 같이 첫번째 idx까지 비교가 끝나면 그 다음(3번째)으로 넘어가 똑같은 과정을 반복하고, 마찬가지로 n번째 까지 끝내면 된다.
Time complexity
- Best case(이미 정렬)의 경우 pivot을 n-1번(2번째부터 n까지) 선정하고 한번의 비교로(pivot 앞의 수가 자신보다 작으면 더 앞의 수 모두 자신보다 작다) 끝나기 때문에 O(n)의 Time complexity를 가지게 된다.
- Worst case(역순 배치)의 경우 pivot을 n-1번 선정하고 각각의 pivot마다 n번 비교를 하고 swap이 일어나게 되므로 (n-1)+(n-2)+ ... +2+1 = n(n-1) * 1/2 즉 O(n^2)이 된다.
- Avg time complexity = O(n^2)
Implementaion
간단한 C++ 구현 예시
#include <stdio.h>
#include <iostream>
using namespace std;
int arr[10] = { 15,3,643,25,1,23,4,9,124,58 };
void insertion_sort(int arr[],int size) {
int i, j, pivot;
for (i = 1; i < size; i++) {
pivot = arr[i];
for (j = i-1; j >= 0 && arr[j] > pivot; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = pivot;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
insertion_sort(arr, 10);
for(int i=0; i<10; i++)
cout << arr[i] << "\n";
return 0;
}정리
Insertion sort같은 경우 뒤에 나오는 selection sort와 상당히 유사한 부분들이 많기 때문에 공통점과 차이점을 비교해보면 좋을 것 같다. 이에 관해서는 Selection sort의 정리부분에 간단히 기술하였다.
Selection sort
정렬방법
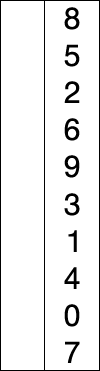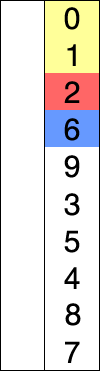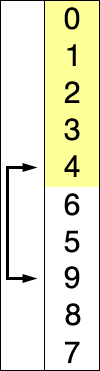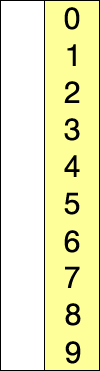
https://en.wikipedia.org/wiki/Selection_sort
- 위에 나왔던 insertion sort와 같이 pivot을 정하는데, 제일 첫번재값부터 순서대로 정한다.
- 그 후, pivot값을 제외한 나머지 배열에서 최소값을 찾는다.
- 찾은 최솟값과 pivot을 비교한뒤 pivot의 값보다 작으면 위치를 바꾸고, pivot 자신이 최솟값이면 다음 pivot으로 넘어가서 반복한다. (이 때, 제일 마지막 값은 자동으로 정렬되기 때문에 n-1번만 하면된다.)
Time complexity
1...n-1의 수까지 반복적으로 최소값을 찾고 swap하는과정에서 (n-1)+(n-2)+ ... +2+1 = n(n-1) * 1/2 즉 O(n^2)의 time complexity를 가진다.
Implementation
#include <stdio.h>
#include <iostream>
using namespace std;
int arr[10] = { 15,3,643,25,1,23,4,9,124,58 };
void swap(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
void selection_sort(int arr[],int size) {
int i, j, min;
for (i = 0; i < size - 1 ; i++) {
min = i;
for (j = i+1; j < size; j++) {
if (arr[j] < arr[min])
min = j;
}
if (min != i)
swap(arr[i], arr[min]); //arr[i] = pivot
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
selection_sort(arr, 10);
for(int i=0; i<10; i++)
cout << arr[i] << "\n";
return 0;
}정리
Selection sort의 경우 Insertion sort와 방식에 있어 상당한 유사점을 가진다. pivot 이전의 순서의 배열은 다 정렬이 된 상태이며 k번째 반복이 끝나고 k+1번째 수를 정렬하기 위해 1번째~k번째 수를 비교하느냐 k+1~n번째 수를 비교하느냐의 차이점이 있다. Insertion sort는 비교의 횟수가 swap의 횟수보다 적고, Selection sort는 비교의 횟수가 swap의 횟수보다 많다. 즉, 이미 정렬된 정도가 클수록 insertion sort에서의 이득이 크다.
Insertion, Selection sort 모두 O(n^2)의 time complexity를 가지므로 배열이 커질수록 성능이 떨어진다. 하지만 아주 작은 수(1-20정도)에서는 quick sort(O(nlogn))보다 빠른 속도를 보여주기 때문에 충분히 작은 sublist를 가지는 재귀함수 등에서 유용하게 쓰일 수 있다.
마치며
이번에는 가장 기본적인 algorithm인 sorting algorithm중에서도 구현이 간단한 Bubble, Insertion, Selection sort를 살펴보았다.
추후에 배울 다른 sorting algorithm들 보다 중요도는 덜하겠지만 그렇다고 몰라도 되는건 절대 아니니 잘 기억하면 좋을 것 같다.