Merge Sort
정렬방법
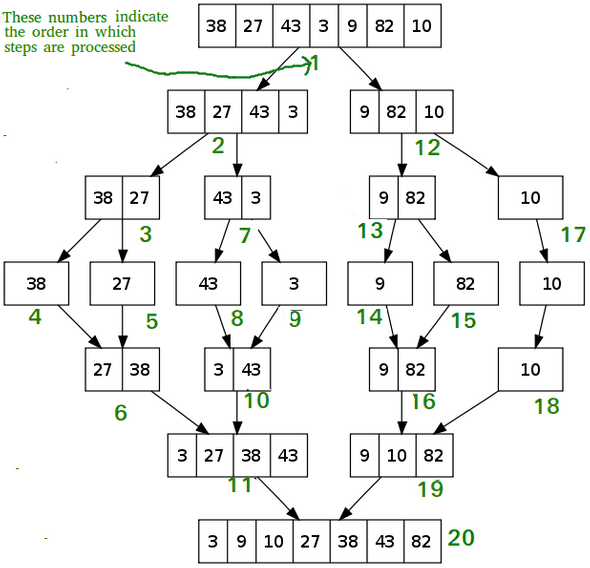
Merge sorting은 divide and conquer 알고리즘 중 하나이다.
기본적으로 array를 여러개의 sub array로 나누는 divide, 각각의 sub array들을 정렬하는 conquer, 그리고 sub array들을 다시 하나의 array로 합치는 merge(combine) 과정을 거친다.
- array를 반으로 잘라 원소가 1개가 될 때 까지 계속 sub array로 나눈다.
- 모든 원소가 1개가 되면 divide를 멈춘다.
- 작은수를 왼쪽, 큰수를 오른쪽에 두며 conquer&combine(정렬,합병)을 시행한다.
- 이 때 원소가 2개이상의 배열을 합칠 때에는 아래와 같이 시행한다.
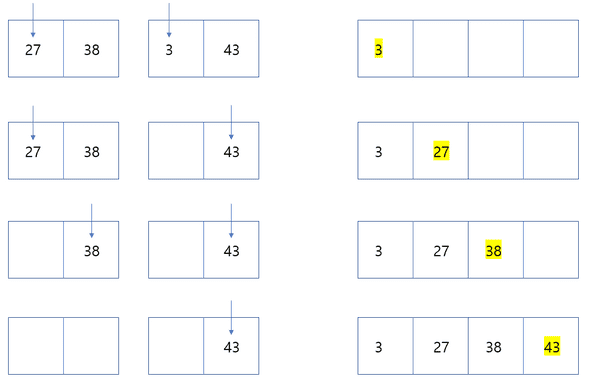
각 array의 값들을 처음부터 하나씩 비교하면서 더 작은수를 sorted array에 넣는다. 위에서 넣은 array의 비교 대상을 오른쪽으로 옮기고 다시 다른쪽 array와 차례대로 비교한다.
이 때 한쪽의 array의 원소가 먼저 모두 사라지면 남은쪽 array의 원소들을 모두 sorted array 오른쪽에 넣으면 된다.(남은쪽 array의 제일 작은수가 다른쪽 array모든수보다 제일 크다.)
그림에서도 유추할 수 있듯이 merge sorting은 재귀함수로 진행된다. 이 부분은 코드를 함께 보면 더욱 직관적으로 이해할 수 있다.
재귀함수를 다시 올라가며 나머지 sub array들도 merge하면 최종적으로 정렬이된 sorted array를 얻을 수 있다.
Time complexity
merge sort는 array를 2등분 하는 재귀함수이기 때문에 순환호출에 있어O( log(n)), 각 순환호출 안에서 array를 merge하는데 O(n)이므로 총 O(nlogn)의 time complexity를 가진다.
Implementation
c/c++ 간단한 구현 예제
#include <stdio.h>
#include <iostream>
using namespace std;
int arr[11] = { 15,3,643,25,1,23,4,9,124,58, 55 };
int sorted_arr[11];
void merge(int arr[], int p, int q, int r) {
int i = p, j = q+1, k = p;
while (i <= q && j <= r) { // 둘중 하나의 배열이 empty 될 때까지 반복
if (arr[i] > arr[j])
sorted_arr[k++] = arr[j++];
else
sorted_arr[k++] = arr[i++];
}
while (i <= q ) { //오른쪽이 먼저 없어졌을때 왼쪽 나머지를 배열에 복사
sorted_arr[k++] = arr[i++];
}
while (j <= r) { // 위와 반대
sorted_arr[k++] = arr[j++];
}
for (int l = p; l <= r; l++) { //원래 배열에 값 복사
arr[l] = sorted_arr[l];
}
}
void merge_sort(int arr[],int p, int r) { //p = leftmost, r = rightmost
int q; //q = mid
if (p < r) { // p = r -> one element
q = (p + r) / 2;
merge_sort(arr, p, q);
merge_sort(arr, q + 1, r);
merge(arr,p,q,r);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
merge_sort(arr,0,10);
for(int i=0; i<11; i++)
cout << arr[i] << "\n";
return 0;
}정리
merge sort는 stable sorting algorithm이다.
insertion, quick sorting과는 다르게 배열의 이미 정렬된 정도에 상관없이 항상 비슷한 time complexity를 갖는다. (insertion, quick은 배열이 이미 정렬된 정도에 따라 차이가 심함.)
또한 배열을 나누고 합치는데 추가적인 메모리 공간이 필요하므로 제자리 정렬이 아니다. 하지만 array를 linked-list로 구현한다면 이동횟수를 획기적으로 줄이고 제자리 정렬로 구현이 가능하다.