1. Linear Algebra - (2)

Vector Space

Matrix는 Vector를 변환하거나 Vector Space를 정의하는 등 Matrix와 Vector는 매우 밀접한 연관이 있다.

Group

Definition of Group:

• Consider a set $\mathcal{G}^4$ and an operator $\otimes$ : $\mathcal{G}$ × $\mathcal{G}$ → $\mathcal{G}$ defined on $\mathcal{G}$. Then G := ($\mathcal{G}$, $\otimes$) is called group if the following holds:

  • Closure(닫힘성): 어떠한 Operation $\otimes$ 에 대하여 $\forall{x,y}\in\mathcal{G}$ 인 $x, y$ 에 대하여 $x\otimes y \in \mathcal{G}$ 이다.
  • Associativity(결합법칙): $\forall{x,y,z}\in\mathcal{G}$ 에 대하여 $(x\otimes y) \otimes z = x\otimes (y \otimes z)$ 이다.
  • Neutral element(중립원) or Identity element: $\exists{e}\in\mathcal{G},\ \forall{x}\in\mathcal{G}$: $x\otimes e = x$ and $e\otimes x = x$
  • Inverse element(역원): $\forall{x}\in\mathcal{G},\ \exists{y}\in\mathcal{G}$ : $x\otimes y = e$ and $y\otimes x = e$ 이면 $y = x^{-1}$를 $x$ 의 inverse 라고 부른다.
  • Commutative(Abelian group): $\forall{x,y}\in\mathcal{G}$: $x\otimes y = y\otimes x$. 벡터공간에서의 덧셈은 아벨군이라고도 부름.

Vector Group의 예시는 다음과 같다.

1. $(\mathbb{Z},+)$ 는 Group이다.

   • Closure: 두 정수를 더하면 여전히 정수임.
   • Associativity: 정수의 덧셈은 결합 법칙을 만족.
   • Neutral element: 0.
   • Inverse element: $x, -x$

2. $(\mathbb{N}_0, + )$ 는 Group이 아니다.

   • Inverse element 가 존재하지 않는다. (e.g. <0, 1>)

3. $(\mathbb{Z},\cdot)$ 는 Group이 아니다.

   • Inverse element 가 존재하지 않는다. (e.g. <4, 1> → inverse = 1/4)

4. $(\mathbb{R}, \cdot)$ 는 Group이 아니다.

   • Inverse element 가 존재하지 않는다. (e.g. <0, 1>)

5. $(\mathbb{R^{m\times n}}, +)$ 는 Abelian Group 이다.

   • 실수 행렬에 대해서 덧셈은 조건들을 만족함.

($\mathbb{Z}$=정수, $\mathbb{N}_0$=0을 포함한 자연수)

Vector Spaces

Definition of Vector Space:

• A real-valued vector space $V=(\mathcal{V}, +, \cdot)$ 는 다음과 같은 두가지 연산이 정의된 set $\mathcal{V}$ 이고

  • Vector Addition : $\mathcal{V}+\mathcal{V}→\mathcal{V}$
  • Scalar multiplication : $\mathbb{R}\times \mathcal{V}→\mathcal{V}$

• 이 두가지 연산이

  • $(\mathcal{V}, +)$ is an Abelian group

  • Distributivity:

    $\ \forall{\lambda}\in\mathbb{R},\ x,y\in\mathcal{V}$ : $\lambda\cdot(x+y)=\lambda\cdot x+\lambda\cdot y$

    $\forall{\lambda,\psi}\in\mathbb{R},\ x\in\mathcal{V}$: $(\lambda+\psi)\cdot x = \lambda\cdot x + \psi\cdot x$

  • Associativity: $\forall{\lambda,\psi}\in\mathbb{R},\ x\in\mathcal{V}$: $\lambda(\psi\cdot x) = (\lambda\psi)\cdot x$
  • Neutral element with respect to the dot operation: $x\in\mathcal{V}$ : $1\cdot x=x$

  위의 네 가지를 모두 만족하면 $\mathcal{V}$ 는 Vector Space이다.

추가적으로 Vector Subspace 의 정의는 다음과 같다.

• Let $V = (\mathcal{V}, +, \cdot)$ be a vector space and $\mathcal{U} \subseteq \mathcal{V}$, $\mathcal{U} \neq \emptyset$. Then $\mathcal{U}=(\mathcal{U},+,\cdot)$ is called vector subspace of $V$ (or linear subspace) if $\mathcal{U}$ is a vector space with the vector space operations + and $\cdot$ restricted to $\mathcal{U} \times \mathcal{U}$ and $\mathbb{R}\times \mathcal{U}$ (closed). We write $U \subseteq V$ to denote a subspace $\mathcal{U}$ of V

예를 들어,

The solution of a homogeneous system of linear equations $Ax = 0$ with unknown $x$ is a subspace of $\mathbb{R}^n$ 이다.

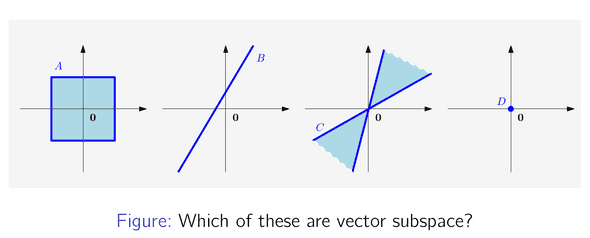
아래의 그림에서는 Vector space $(\mathbb{R}^2, +, \cdot)$ 에 대하여 A, B, C, D 중 D만이 Vector subspace이다.

---

Linear Independence

Linear Combination

Definition of Linear Combination:

• Vector Space $V$ 의 vectors $x_1, x_2, …, x_k \in V$ 와 scalars $\lambda_1, \lambda_2, …, \lambda_k \in \mathbb{R}$ 에 대하여 이 둘의 조합 $v = \sum_{i=1}^k \lambda_i x_i \in V$ 를 Linear Combination 이라고 한다.

Linear (In)dependence

Definition of Linear (In)dependence:

• Let us consider a vector space V with $k \in \mathbb{N}$ and $x_1 , ..., x_k \in V$ . If there is a non-trivial linear combination, such that $0 = \sum_{i=1}^k \lambda_i x_i$ with at least one $\lambda_i \neq 0$, the vectors $x_1 , ..., x_k$ are linearly dependent. If only the trivial solution exists, i.e., $\forall\lambda_i = 0$, the vectors $x_1 , ..., x_k$ are linearly independent
• 즉 Linearly independent 하려면, 어떤 vector도 나머지 vector들의 linear combination으로 나타낼 수 없음을 의미함. ($\lambda_i x_i = 0$ 의 해가 모든 Scalar가 0이 되는것 뿐)
• Row-Echelon Form 의 형태를 만들면, 해당 Vector의 Linear (In)dependence 를 체크할 수 있다.

---

Basis and Rank

Span

Definition of Generating set and Span:

• Consider a vector space $V = (\mathcal{V}, +, \cdot)$ and set of vectors $A = \{x_1 , ..., x_k\} \ \subseteq \mathcal{V}$. If every vector $v \in \mathcal{V}$ can be expressed as a linear combination of $x_1 , ..., x_k$ , $\mathcal{A}$ is called a generating set of $V$. The set of all linear combinations of vectors in $\mathcal{A}$ is called the span of $\mathcal{A}$. If $\mathcal{A}$ spans the vector space $V$ , we write $V = span(\mathcal{A})$ or $V = span(x_1 , ..., x_k)$

즉 Vector Space $V$ 안에 존재하는 Vector $\mathcal{V}$ 들로 구성된 임의의 set $\mathcal{A}$ 에 대하여, Vector space 안의 모든 Vector가 set $\mathcal{A}$ 안의 vector들의 linear combination 으로 표현이 가능하다면 $\mathcal{A}$ 는 $V$ 의 generating set이다. 즉, $\mathcal{A}$ 안의 vector 들이 Vector space $V$ 를 생성한다.

$\mathcal{A}$ 안에 포함된 모든 벡터들의 linear combination을 $\mathcal{A}$ 의 span 이라고 하며, 만약 $\mathcal{A}$ 의 span이 Vector Space $V$ 와 같다면 $V = span(\mathcal{A})$ 라고 표현할 수 있다.

Basis

Definition of Basis:

• Consider a vector space $V = (\mathcal{V}, +, \cdot)$ and $\mathcal{A} \subseteq \mathcal{V}$. $A$ generating set $\mathcal{A}$ of $V$ is called minimal if there exists no smaller set $\mathcal{A}^′ \subseteq \mathcal{A} \subseteq \mathcal{V}$ that spans $V$ . Every linearly independent generating set of $V$ is minimal and is called a basis of $V$ .

즉 Basis는 Vector Space $A$ 에 대한 minimal generating set의 linear independent vector set 라고 할 수 있다.

(e.g. $\mathbb{R}^2, \mathcal{B} = \{\mathbf{e}_1, \mathbf{e}_2 \}$)

Vector들의 Linear independence를 파악하기 위해서, 앞서 배운 Gaussian elimination을 사용할 수 있다.

Gaussian elimination을 거치면 Vector는 RREF 형태로 나오게 되고, 모든 Column에 대해서 Pivot이 존재한다면 linear independent 하다.

예를 들어, 위의 $\mathcal{B_2}$ 를 RREF로 만들면 $\mathcal{B}_2 = \{ [1, 0,0]^T, [0, 1 ,0]^T, [0,0,1]^T\}$ 가 되므로 linearly independent하고 각 vector로 $\mathbb{R}^3$ 공간 상의 모든 Vector를 표현할 수 있는 mininmal generating set이므로, $\mathbb{R}^3$ 의 Basis 라고 할 수 있다.

Dimension and Rank

Definition of Dimension:

• There can be many basis of a vector space.
• However, all bases possess the same number of basis vectors.
• The number of basis vectors are called dimension of the vector space.
• The dimension is not necessarily the number of elements in a vector.

즉 Dimension은 해당 Vector Space를 생성하기 위한 최소한의 Vector 수 를 뜻하며, 이는 곧 Basis 의 vector 수를 의미한다.

Definition of Rank:

• The number of linearly independent columns of a matrix $A \in \mathbb{R}^{m×n}$
• (=) The number of linearly independent rows of a matrix $A \in \mathbb{R}^{m×n}$
• The columns of $A$ span a subspace $U \subseteq \mathbb{R}^m$ with $dim(U) = rk(A)$. This subspace is called image or range
• A matrix A has full rank if $rk(A) = min(n, m)$
• A square matrix $B \in \mathbb{R}^{m×m}$ is invertible iff $B$ has full rank

Ref:

• POSTECH CSED343 (Prof. Dongwoo Kim)
• Mathematics for Machine Learning, Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong, Cambridge University Press 2020