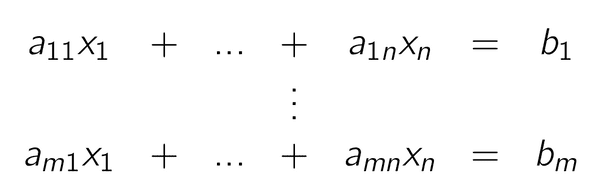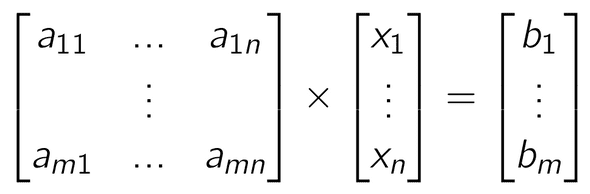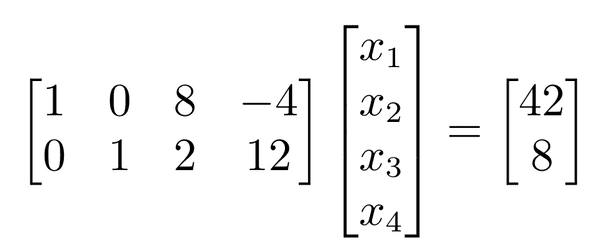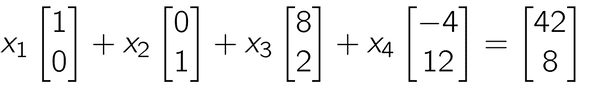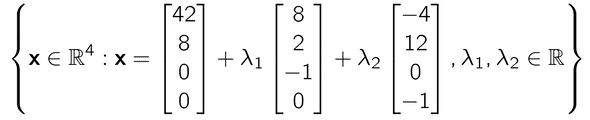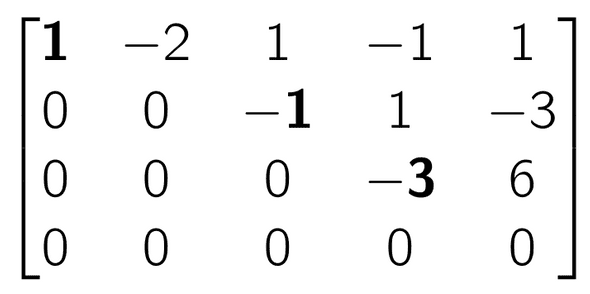1. Linear Algebra - (1)

Matrices

이번 시간에는 기계학습을 위한 수학 중, 선형대 수학의 Matrix 에 대한 기본적인 개념들을 알아본다.

Inverse

Definition of Inverse:

• Consider a square matrix $A\in\mathbb{R}^{n\times n}$, Let matrix $B\in\mathbb{R}^{n\times n}$ have the property that $AB=I_n=BA$.\ $B$ is called the inverse of $A$ and denoted by $A^{-1}$

즉 $n\times n$의 정방행렬 $A$ 에 대하여 행렬곱을 했을 때 Identity matrix가 나오게 하는 정방행렬 $B$ 를 $A$의 inverse matrix 라고 한다.

역행렬은 주어진 행렬이 가역적(invertible)일 때만 존재.

가역성은 행렬식(Determinant) 를 통해서 판단 가능하고 ($det(A) !=0$ → invertible), 이를 구하기 위해서는 행렬이 정방행렬이여야함.

(p.s. 정방행렬이 아닌 행렬식에서는 Moore-Penrose pseudo-inverse 를 통해서 해를 근사할 수 있음.)

• 모든 matrix가 inverse matrix를 가지는 것은 아니다.
• 만약 inverse matrix가 존재한다면, 그 matrix는 regular/invertible/nonsingular 라고 부른다.
• 만약 존재하지 않는다면, singular/noninvertible 라고 부른다.
  

Transpose

Definition of Transpose:

• For $A\in\mathbb{R^{m\times n}}$ the matrix $B\in\mathbb{R^{m\times n}}$ with $b_{ij} = a_{ji}$ is called the transpose of $A$. We write $B^T = A$

즉 Matrix 원소들의 Row와 Column이 바뀐 상태를 의미한다.

• 만약 matrix $A\in\mathbb{R^{m\times n}}$ 에 대해서 $A=A^T$ 라면 $A$ 는 symmetric 이라고 한다.

vanilla python으로 matrix의 upper triangle만 탐색하여 간단하게 transpose를 구현할 수 있다. (or numpy.array.T)

#nxn matrix
for i in range(n): #row
	for j in range(i+1, n): #col
		matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

Compact representation of system of linear equations

우리는 Matrix와 Vector를 사용하여 linear equations를 표현할 수 있다.

아래와 같은 Linear equation은

아래와 같이 $Ax=b$ 형태의 Matrix와 Vector 로 표현될 수 있다.

예를 들어

위의 System은 2개의 equation과 4개의 unknown variable이 존재한다. (즉 무수한 해(solutions)가 존재)

이 문제는 마찬가지로 $\sum_{i=0}^4 x_ic_i=b$ 의 형태로 표현할 수 있는데, 여기서 $c_i$는 $i$번째 Column이고 $b$ 는 $[42, 8]^T$ 이다.

그럼 이 식을 어떻게 풀 수 있을까?

Particular Solution

Particular Solution(특별해)은 말 그대로 어떠한 Linear equation system을 만족하는 하나의 특정한 해 이다.

예를 들어 바로 앞전의 linear equation $\sum_{i=0}^4 x_ic_i=b$ 에서

위 linear equation을 만족하는 해는 single 1 을 포함하는 column들을 통해서 쉽게 구할 수 있으며 이 경우 $x=[42, 8, 0, 0]^T$ 가 될 것이다.

General Solution

General Solution(일반해) 는 Linear equation system을 만족하는 모든 해들의 집합 을 나타낸다.

간단한 아이디어로, Linear equation에서 이미 구한 Particular solution에 0을 더하는 것은 기존 해가 성립하는데 에 있어서 아무런 영향을 주지 않을것이다.

따라서 이를 이용하여 Particular solution에서 사용되지 않는 변수 (위의 예제에서 $x_3, x_4$) 를 linear combination으로 표현하고, 자유변수 $\lambda_i$ 를 사용하여 homogeneous solution 을 추가해 더 많은 해들의 집합 $\lambda$ 를 구할 수 있다.

앞선 예제에서 $x_3[8, 2]^T$ 는 $8\times [1, 0]^T$ (which is $c_1$) + $2\times [0, 1]^T$ (which is $c_2$) 로 나타낼 수 있다.

$\therefore$ $\lambda_1(8c_1+2c_2-c_3)=0$

마찬가지로 4번째 항도 아래와 같이 표현 가능하다.

$\therefore\lambda_2(-4c_1+12c_2-c_4)=0$

최종적으로 general solution은 아래처럼 표현 가능하다.

Row-Echelon Form

Linear equation의 Solution을 구할때에는 Matrix를 Reduced Row-Echelon Form으로 만들면 매우 유용하다.

여기서 (Reduced) Row-Echelon Form은 뭘까?

Definition of Row-Echelon Form (REF):

• All rows that contains only zeros are at the bottom of the matrix; correspondingly, all rows that contains at least one nonzero element are on top of rows that contain only zeros.
• Looking at nonzero rows only, the first nonzero number from the left (also called pivot) is always strictly to the right of the pivot of the row above it.

참고: REF 에서 Pivot value에 대한 정의가 다른 경우가 있다.

*Technically, the leading coefficient can be any number. However, the majority of Linear Algebra textbooks do state that the leading coefficient must be the number 1. To add to the confusion, some definitions of row echelon form state that there must be zeros both above and below the leading coefficient. It’s therefore best to follow the definition given in the textbook you’re following (or the one given to you by your professor). ref;* statisticshowto

예를 들어,

위의 Matrix는 모든 Pivot 이 이전 row 의 Pivot 위치보다 오른쪽에 있고,

모든 값이 0인 Row가 제일 밑에 존재하므로 Row-Echelon Form 이라고 할 수 있다.

Definition of Reduced Row-Echelon Form (RREF):

• It is in row-echelon form
• Every pivot is 1.
• The pivot is the only nonzero entry in its column.

예를 들어,

위의 Matrix는 1) 모든 Pivot value가 1이고, 2) 이전 row의 Pivot보다 오른쪽에 있으며, 3) 각 Pivot의 Column은 pivot이외의 값들이 모두 0이기 때문에 Reduced Row-Echelon Form 이라고 할 수 있다.

Reduced Row-Echelon Form에서는 Linear equation의 해를 매우 쉽게 구할 수 있다.

각각의 $i$ 번째 Pivot이 $x_i$ 의 해를 나타내므로

$x_1 = -2,\ x_3=1,\ x_4=-2$ 이고 Pivot이 존재하지 않는 2번째 Column은 free variable이 되므로 단순히 0 을 대입해 $x_2=0$ 을 얻으면 하나의 Particular Solution을 얻을 수 있다.

Free variable을 활용한 General Solution도 마찬가지로 아래와 같이 구할 수 있다

$x_1=2x_2-2,\\ x_3=1,\\ x_4=-2$

여기서 $x_2$ 는 Free variable이므로 $x_2=\lambda$라고 하면

$(x_1, x_2, x_3, x_4)=2\lambda-2,\ \lambda, 1,\ -2$

즉 $x\in\mathbb{R}^4 : x= [-2, 0, 1, -2]^T + \lambda[-2, -1, 0, 0]^T$

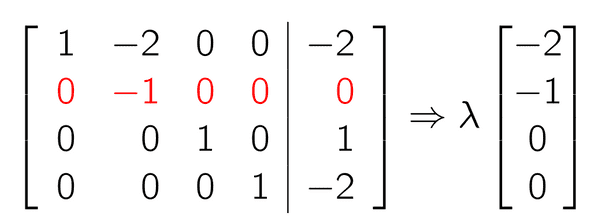
혹은 Minus one Trick을 사용하여 직관적으로 구할 수도 있다.

Free variable이 위치하는 Column에 -1 을 넣어주면

마찬가지로 $x\in\mathbb{R}^4 : x= [-2, 0, 1, -2]^T + \lambda[-2, -1, 0, 0]^T$ 를 얻을 수 있다.

Reduced Row-Echelon Form을 만드는 방법으로는 Gaussian elimination algorithm을 사용하면 된다.

Ref: Wikipedia

Ref:

• POSTECH CSED343 (Prof. Dongwoo Kim)
• Mathematics for Machine Learning, Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong, Cambridge University Press 2020