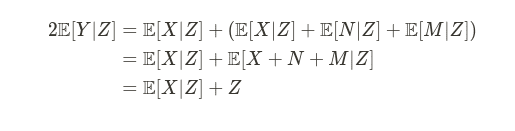Noisier2Noise: Learning to Denoise from Unpaired Noisy Data

Noisier2Noise

Intro

Deep learning image denoising task 에서는 일반적으로 noise image - clean image 를 pair로 갖는 data에 대해서 학습하였습니다.

하지만 이러한 condition의 image pair를 취득하는것은 매우 까다로운 일이기 때문에 Noise2Noise 처럼 noise image들로만 학습하는 방법론이 소개되었습니다.

Nooisier2Noise 에서는 더 나아가 pair data가 필요 없는 single noise image로 denoising network를 학습하는 방법을 제시합니다.

Method

Random distribution $\mathcal{A}$ 로부터 얻어진 random variable $M,N$ 이 있다고 가정해봅시다.

$Z=M+N$ 에 대해서 $N$ 을 예측한다고 할 때, $N$ 의 근사값 $\mathbb{E}[N|Z]$ 를 구하는것에 있어 $M, N$ 는 같은 distribution $\mathcal{A}$ 로부터 얻어졌기 때문에 각각 추측된 값에 대한 그 반대 조합도 symmetric 하게 존재합니다.

결국 두 추측값의 평균은 $N=M=\frac{z}{2}$가 될것이며, 이것이 Noisier2Noise에 있어서 핵심적인 포인트입니다.

위의 과정을 두개의 i.i.d noise sample 에도 그대로 적용할 수 있습니다.

i.i.d noise sample $M, N$ 에 대해서 $Z=M+N$ 이라고 할 때, 주어진 unknown quantity $x$ 에 대해서 $x+Z$ 를 가지고 $x+N$ 을 예측한다고 가정해봅니다.

그렇다면 최적 예측값은 마찬가지로 $x+\frac{Z}{2}$ 에 수렴할것이고, 이것은 $x, x+Z$ 의 중간값 입니다. 그러므로 이 값들을 통해서 $x$ 를 근사할 수 있습니다.

중요한 것은, 이러한 점을 그대로 Image denoising의 관점에 대입할 수 있다는 것입니다.

Clean image $x$, Noise image $x+N$, Noisier image $x+N+M=x+Z$ 이라고 할때, 우리는 noisy image $x+N$ 과 같은 noise distribution을 추가해 만든 noisier image $x+Z$ 를 통해 clean image $x$ 를 구할 수 있다는 결론을 도출할 수 있습니다.

Noisier2Noise는 noise image $Y=X+N$, noisier image $Z=Y+M$ 라고 할 때, noisier Input $Z$ 를 통해서 noise image $Y$를 예측하는 task입니다.

natural image distribution $\mathcal{X}$ 에 대한 $X\sim\mathcal{X}$ 가 존재할때, $X$ 를 직접 볼 수 없지만 known noise distribution $\mathcal{A}$ 에 대한 noise $N\sim\mathcal{A}$ 이 추가된 $Y=X+N$ 은 얻을 수 있습니다. $\mathcal{A}$ 가 known distribution이므로, synthetic noise sample $M\sim\mathcal{A}$ 을 생성하여 noisier image $Z$ 를 합성할 수 있습니다.

이것을 Deep learning process에 도입하여 $L_2$ loss 를 사용하여 neural network $f(;\theta)$ 를 통해 input $Z$ 로 $Y$ 를 예측하는 과정을 아래와 같이 정의할 수 있습니다.

$\argmin_\theta\mathbb{E}[\parallel f(Z;\theta)-Y \parallel_2]$

Loss function을 최소화 하는 가장 좋은 정답은 $Z$ 에서 정확히 $M$ 을 구해서 빼주는것이지만, network는 $N, M$ 중 어떠한 것도 관찰하지 못했기 때문에 불가능하며, $\mathbb{E}[Y|Z]$ 를 근사하는것이 최선이라고 할 수 있습니다.

이 때, $M,N$ 이 i.i.d 이기 때문에 $\mathbb{E}[M|Z] = \mathbb{E}[N|Z]$ 이므로 아래와 같은 식을 유도할 수 있습니다.

위의 식을 통해서 $\mathbb{E}[X|Z]=2\mathbb{E}[Y|Z]-Z$ ,즉 Model의 Output * 2 - Input 을 통해서 clean image $x$ 를 구할 수 있다는것을 알 수 있습니다.

$\mathbb{E}[X|Z]$ 가 정확한 true image로 reconstruct된다는 것은 보장할 수 없지만, 적어도 clean images 후보들의 mean으로 향하게될것이고, 이는 noise 2 clean 의 학습에 있어서도 마찬가지 현상입니다.

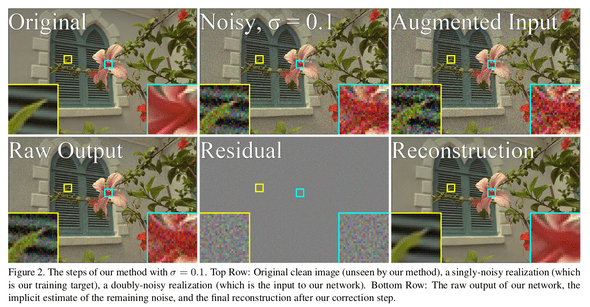
아래의 과정을 통해서 앞에서 설명한 가정이 올바름을 확인할 수 있습니다.

1. Augmented Input $z$ 를 network에 통과시켜 $f(z;\theta)$ 를 얻습니다. $f(z;\theta)$ 는 clean image $x$ 가 아니라 $x$ 와 $x+n$ (noisy) 의 중간으로 가기 때문에 아직 noise가 남아있는것을 확인할 수 있습니다.
2. $z-f(z;\theta)$ 를 통해 남아있는 estimate noise 를 얻습니다. noise의 양상을 통해 이 noise의 표준편차가 $\frac{\sqrt{2}\sigma}{2}$ 를 따른다고 추측할 수 있습니다.
3. 위의 noise를 $f(z;\theta)$ 에 빼주어 $2f(z;\theta) - z$ = Output * 2 - Input 을 계산합니다.
4. 최종적으로 Reconstruct된 estimate clean image 를 확인할 수 있습니다.

Improvement

Noisier2Noise 방법으로 학습된 model은, Input으로 doubly-noisy (Noisier) image를 받는다는 한계점이 있습니다.

이로인해 model이 원래의 noisy image에 대해서 정확한 참고를 할 수 없기때문에, 저자는 이 문제를 해결하기 위한 두가지의 방법을 제시합니다.

Inference unaugmented (singly) noisy image

간단하게 생각해볼 수 있는 첫번째 방법은, inference 시 image에 추가적인 noise를 더하지 않는것입니다.

model이 random patch image로 학습하기 때문에 어떠한 데이터는 다른 데이터와 비교했을 때 더 적은 noise 를 가지고있을것입니다.

model은 이러한 데이터 또한 denoising 할 수 있는 능력을 학습하기 때문에 image 전체가 더 적은 noise를 가지고 있어도 충분히 denoising 할 수 있다고 가정할 수 있습니다.

하지만 실혐결과, singly-noisy image로 inference 했을 경우 PSNR 수치는 소폭 상승하지만 over-smoothing으로 인해서 detail이 많이 사라지는것을 확인할 수 있었습니다.

Changing noise intensity

두번째 방법은 noisy image보다 더 적은 정도의 noise를 더해주는것입니다.

앞선 과정들에서 우리는 표준편차 $\sigma_\mathcal{A}$ 를 가진 noise distribution $\mathcal{A}$ 에 대해서 synthetic noise $M\sim\mathcal{A}$ 를 생성했습니다.

대신, $\sigma_\mathcal{B} < \sigma_\mathcal{A}$ 인 distribution $\mathcal{B}$ 에 대해서 noise $M \sim \mathcal{B}$ 를 생성하는 방법이 있습니다.

이를 통해서 synthetic noise $M$ 을 통해 image가 왜곡되는 정도가 줄어들고, model은 target noisy image 그 자체에 대해서 참고를 더 많이 할 수 있게 됩니다.

synthetic noise distribution 이 바뀌게 되면 $\mathbb{E}[Y|Z]$ 의 값들도 바뀌게 되는데, 이는 correction step 또한 바뀌어야함을 의미합니다.

$\sigma_\mathcal{B} = \alpha\sigma_{\mathcal{A}}$ , zero-mean인 gaussian $\mathcal{A}, \mathcal{B}$ 에 대해서 correction step은 Lemma 3.1. 로 정리할 수 있습니다.

논문에서는 실험을 통해 $\alpha=0.5$ 일때 general 하게 좋은 성능을 보여주며, fine tuning을 통해 새로운 $\alpha$ 값으로 학습될 수 있다는것을 알아냈습니다.

Experiments

논문에서는 Noise2Noise와 같은 Unet 구조의 network를 사용하여 학습과 테스트를 진행하였습니다.

Noise intensity

각각의 gaussain noise에 $\alpha=0.5$ 를 사용하여 denoising을 했을 때의 결과입니다.

$L_2$ loss의 사용으로 인해서, input에 noise가 많아질수록 증가한 불확실성들의 mean으로 학습이 되기 때문에 detail이 사라지고 smooth 해지는 경향을 보이는것을 확인할 수 있습니다.

Other noises

논문에서는 gaussian noise외에도 bernoulli, structured noise에 대해서도 실험을 하였고, 효과가 있음을 보여주었습니다.

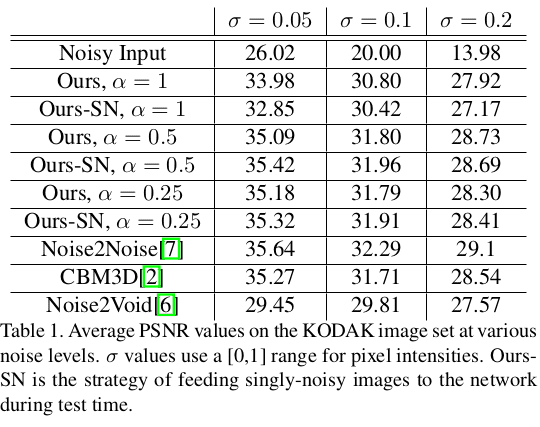
Compare with other models

BM3D, Noise2Noise, Noise2Void 와의 PSNR 비교를 하였습니다. Train data에 대한 requirement가 다르기 때문에 공평한 비교라고 볼수는 없지만, 좋은 성능을 보여주는것을 확인할 수 있습니다.

Discussion

• Real noise에 적용하기 위해서는 noise distribution을 알아야 한다는 말인가? 어떻게 알 수 있는가? 만약 synthetic image에만 적용할 수 있으면 굳이 n2n을 놔두고 이걸 쓸 이유가 있는가?
• PSNR 비교표에서 singly-noisy image를 inference 한것임. 각 sigma에 대한 visualize된 정확한 결과 비교가 없음.