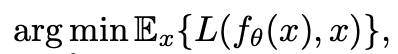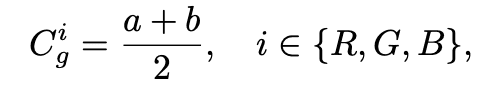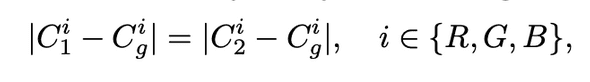NoiSER : Noise is All You Need for Low-Light Image Enhancement

Paper: https://arxiv.org/pdf/2211.04700.pdf

Github: None

이 모델의 가장 큰 특징은, 학습에서 그 어떠한 task related data를 필요로 하지 않고 오직 Noise만 사용한다는 점입니다.

저자는 Task에 관련된 그 어떠한 data도 학습에 사용하지 않는다는 점으로 인해,

• data의 quality에 의해 학습 결과의 질이 결정되는 잠재적 위험을 피할 수 있다.
• 이와 같은 간단한 solution을 활용하여 다른 vision task (denoising, detection 등) 에 대한 joint processing을 깔끔하고 쉽게 가능하게 한다.

위와 같은 장점을 가진다고 주장합니다.

(저는 Over exposure에 대한 robustness, light weight가 그나마 장점이라고 생각합니다.)

---

Preliminaries

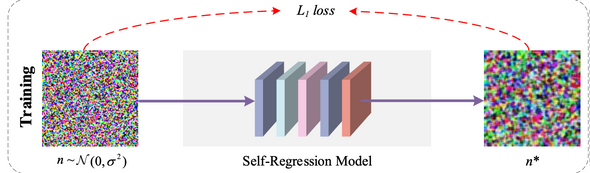
• Image Self-Regression Principle

  Image self regression은 input data 자체를 Output으로 reconstruct하는 supervised signal로 사용하며, 과정을 식으로 나타내면 아래와 같습니다.

  

  학습 과정 이후, 임의의 input $x_0$ 에 대해서 $f_{\theta}$ (model)는 texture-similar output $x^{*}_{0}$ 의 ouput을 배출할 수 있습니다.

  논문에서는 parameterized function $f_{\theta}$를 Con 3x3, GELU, InstanceNorm, Tanh로 이루어진 Layer들로 구성하였습니다.

• Gray-World Color Constancy Hypothesis

  Gray-world hypothesis는 다양한 색 분포를 가지고 있는 Image는, RGB의 평균값이 항상 일정한 gray value K 로 수렴한다는 내용입니다.

  Zero-DCE 등의 모델에서, 해당 가설을 Loss로 사용하여 의미있는 결과를 얻었습니다.

  

• Mirror Visual Feedback Therapy

  거울치료 에 대한 내용인데, 그냥 학습 시 task related (LLIE) data를 안써도, LLIE에 있어 의미있는 output을 만들어 낼 수 있다는 것에 대한 정당화를 위해 넣은 내용 같습니다.

---

Methods

논문에서는 Task related data 없이 LLIE를 수행하기 위한 Requirements를 세가지 설정합니다.

1. Task-related data를 사용하지 않아야한다.
2. Model은 reconstruction ability가 있어야한다.
3. Output의 gray world K value는 80-140과 같은 Normal light의 값과 동일하게 맞춰야한다.

저자는 Color Regression, Pallete Regression, Noise Regression의 실험 과정을 통해

individual phenomenon → individual conclusion → universal conclusion → intra-domain validation 의 귀납추론 방식으로 위의 Requirements를 만족시켜 Noise 학습을 통한 Lowlight enhancement 의 타당성을 입증합니다.

이 페이지에서는 각 실험 결과에 대한 특징만 짧게 정리하겠습니다.

---

Color Regression

Color regression에서는 단색의 Pure color ($x$)를 모델에 통과시켜 학습시키고 임의의 이미지 ($x_0$)를 Inference 하였습니다.

Experiments

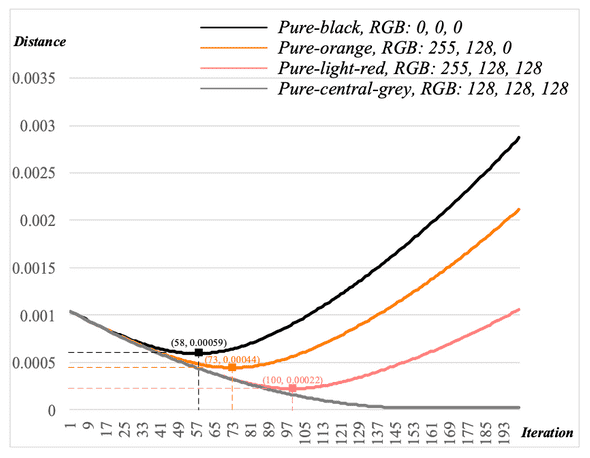
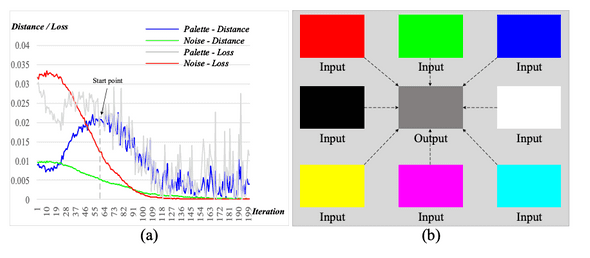
1. Color regresision은 초반 iteration에 pure-gray output을 생성하는 경향이 있습니다.

   

   일정 Iteration 에 대해 Output과 Pure gray에 대한 Distance (L2 loss)를 관찰해보면 초반에 Output이 central gray에 가까워지는 구간이 존재하였고, 이후에 Input color로 수렴하기 시작했습니다. 이는 다른 Pure Color도 마찬가지로 관찰되었습니다.

   여기서 Central gray는 아래와 같이 정의할 수 있으며, 일반적인 rgb space [0, 255] 에서는 (128, 128, 128)이 됩니다.

   

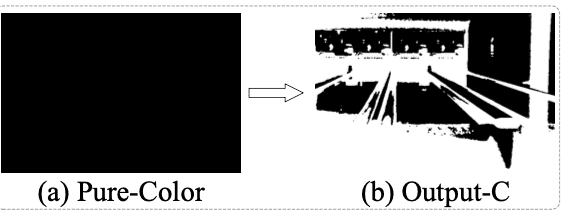
2. Pure color를 계속하여 학습할 시, Inference image를 Binary한 Color로 reconstruct 하게 됩니다.

   

   이 때 Binary color는 1) 학습 시 사용한 Input Pure color, 2) 해당 Pure color의 Opposite color 로 나타났습니다.

   Opposite color는 아래와 같이 정의할 수 있습니다.

   

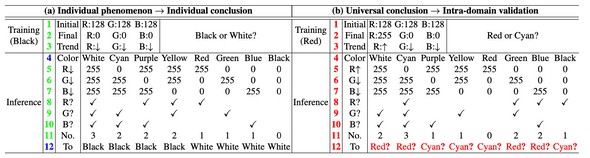
   추가적으로, Color가 Train color 혹은 Opposite color가 되는지는 아래의 표를 통해 추론할 수 있고, 실제로 이러한 양상을 보이는것을 확인할 수 있습니다.

   

   1. 우선 학습에 있어, 초반 Iteration에서 나오는 central gray 의 RGB value에서 목표(Train pure color)로 하는 RGB value 까지의 Trend를 구합니다.
   2. R,G,B에 대해 Inference color가 Target Color가 되기 위해서 앞서 구한 Trend와 2가지 이상 동일하면 Train color로, 그렇지 않을 시 Opposite color로 수렴하게 되는것을 알 수 있습니다.

Conclusion

Color regression을 통해서,

• 해당 모델이 LLIE와 관련 없는 Data를 통해서도 reconstruction을 수행할 수 있으므로 Requirement 1, 2를 만족합니다.
• Color binarisation 현상은 Train color와 연관이 있으며, 이는 곧 sample에 더 많은 색이 포함될수록 더 많은 색과 대비를 가진 결과를 도출할 수 있다고 생각할 수 있습니다.

---

Pallete Regression

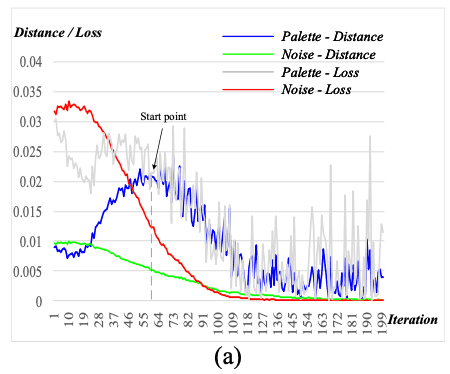
Palette regression에서는 위의 그림과 같이 여러가지 색으로 이루어진 Palette $x$ 를 만들어 학습시키고, 임의의 이미지 ($x_0$)를 Inference 하였습니다.

Experiments

1. Color Regression과 유사한 방법으로 central gray와의 Distance를 구하였을 때, 학습이 진행될수록 Central gray에 수렴되는것을 관찰할 수 있습니다.

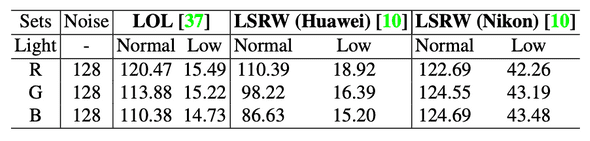
1. LLIE에서 자주 사용되는 Dataset의 high(normal) Image 의 R,G,B 값을 평균내어 봤을 때, 80-140 (~= Central gray) 의 범위를 가지고있었고, 이는 즉 해당 범위의 이미지들은 Normal light (good quality) Image라고 생각할 수 있습니다.

Conclusion

• Pallete regression은 앞서 언급된 Requirements 1,2,3 을 모두 만족하며, 이는 곧 Image enhancement를 수행한다는것을 의미합니다.
• 임의의 Image를 Pallete regression을 통해 학습한 모델에 Inference 했을 때 결과가 불만족 스러운것은 gray world value에 수렴할 때 Loss가 불안정하기 때문이라고 추정할 수 있으며, 이는 곧 Smoothing이 가능하면 결과또한 더 나아질거라고 생각할 수 있습니다.

---

Noise Self Regression

Noise self regression에서는 $I_n \sim N(0, \sigma^2)$ 의 Gaussia Distribution noise $x$ 를 생성하여 모델을 학습하였습니다.

Experiments

1. central gray와의 Distance를 구하였을 때, 학습이 진행될수록 central gray에 수렴되는것을 관찰할 수 있습니다.
2. 모델의 Output에 대한 median value는 Gaussian distribution의 mean값과 정확히 일치합니다. 이는 곧 RGB space에서 normal-light image의 value 평균값을 도출한다고 생각할 수 있습니다.

Conclusion

• Pallete Regression의 특성을 모두 가지므로 Requirements 를 모두 만족하는것은 자명합니다.
• Pallete regression과 같이, Ouput의 RGB값이 central gray로 수렴하는것을 관찰할 수 있고, 훨씬 smooth한 양상을 보입니다. 이를 통해 Inference시 Pallete regression보다 더 나은 품질의 Enhancement를 수행할 수 있다고 생각할 수 있습니다.
• Model의 Instance Normalization layer를 통해서, Input image의 distribution $\mu$ 값이 변하더라도 항상 일관적인 결과를 도출할 수 있습니다.

---

Implementation

위의 실험 결과들을 통해 입증하였듯이, 해당 모델 $f_\theta$에 $I_n \sim N(0, \sigma^2)$ 의 Noise를 넣어 학습시키면 LLIE를 수행할 수 있게 됩니다.

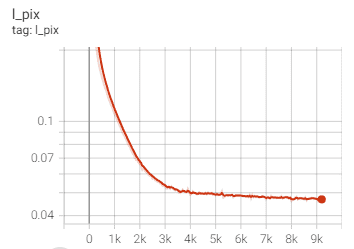
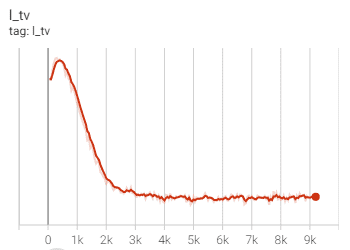
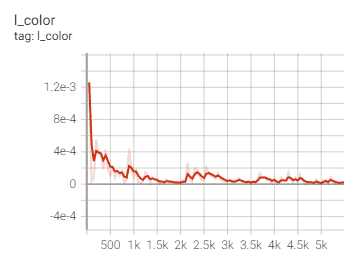
Based on PyTorch 1.10.1 and Python 3.6.9, we train and evaluate our NoiSER on single NVIDIA RTX 2080 Ti GPU. We train our NoiSER for 2000 iterations (600 for NoiSER-ES) with a batch size of 1 and a fixed learning rate of 2e-4. We sam- ple the noise from standard Gaussian distribution N (0, 1) (N (0, 3) for NoiSER-Var3) with a shape of 104 × 104 for training. Besides, the Adam optimizer is utilized for training with β1 = 0.5 and β2 = 0.999. To alleviate the noise in the enhanced results, we add TV regularization during training. The total loss function used in the training of our proposed NoiSER is defined as $L_{total}=L_{l1} + L_{tv}$

Evaluations

Validation

Results

Low Image

Over exposure Image