Deep Neural Networks

Oct 22, 2020

Post Series

Deep Neural Networks

Describe the successive block structure of a deep neural network
Build a deep L-layer neural network
Analyze matrix and vector dimensions to check neural network implementations
Use a cache to pass information from forward to back propagation
Explain the role of hyperparameters in deep learning
Build a 2-layer neural network

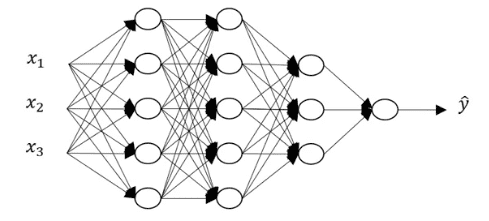
Notation for Deep neural network

Deep neural network라고 해서 앞서 배운 표기법들이 많이 달라지지 않는다.

새로 추가되었다고 볼 수 있는 것들 중 L 은 전체 레이어의 개수를 나타내며 n^[l] 은 l레이어의 히든 유닛 수를 나타낸다.

위와 같은 신경망이 있다고 하자. 그렇다면 L=5, n^[0]=2, n^[1]=5 ... n^[4]=1일 것이다.

Propagation또한 별 다를게 없다. 주의 해야할것은 dimension을 올바르게 유지하면 된다.

예를 들어

Z1 = W1 * X + b1 이라고 하자. 그렇다면 각각의 shape는

W1은 현재 레이어 노드의 개수가 5개이고, 전 레이어로부터의 입력이 3개이기 때문에 (5,3), 즉 (n^[1],n^[0]) 일것이다.

X는 전체 입력값이기 때문에 (3,m) 즉 (n^[0],m) 일 것이다.

b1은 (n^[1],1)인데 , 더할 때 파이썬의 broadcasting으로 인해 자동으로 m만큼 복사가 될 것이다.

따라서 Z1의 shape는 (n^[1],m0) 이 된다.

Vectorization을 요약하자면 Z^[l] = (n^[l],m0), W^[l] = (n^[l],n^[l-1]), b1은 (n^[l],1) 이라고 할 수 있다.

Why Deep Representations?

그렇다면, 이러한 Deep neural network는 그렇지 않은것보다 왜 더 잘 표현하고 잘 학습할까?

그걸 모르면 신경망을 깊고, 크게 구성하는 의미가 없다.

Deep neural network는 기본적으로 많은 layer와 각 layer마다 많은 hidden unit을 포함해야한다.

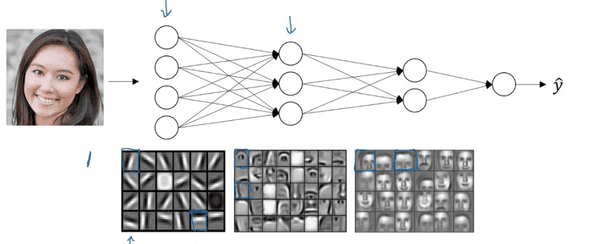
위의 신경망을 살펴보자.

이 신경망은 이미지를 분류하는 CNN(Convolution Neural Network)를 간단히 표현한 것이다.

이 신경망에서는 첫번째 레이어는 아주 작은 단위로 이미지의 꼭지점, 가로경계, 세로경계 등을 구분한다.

그리고 두번째 레이어는 앞서 추출한 특징들을 취합해 조금 더 큰부분을 찾는다. (예를들면 눈, 코 등등..)

그리고 세번째 레이어는 마찬가지로 앞 레이어의 특징들을 합쳐 더 큰 단위로 이미지를 감지한다.

이러한 특징은 이미지 분석 뿐 만 아니라 다른 분야에도 넓게 적용될 수 있고, 그렇기 때문에 Deep neural network가 잘 작동하는 것이다.

Parameters vs HyperParameters

모델의 parameter는 W, b다.

그 외에도 우리가 모델에 알려줘야하는 값들에는 Learning rate, gradient descent할 반복수, hidden layer의 개수, hidden unit의 개수, activation function 등이 있다.

이처럼 W,b를 컨트롤하는 모든 것들을 Hyper Parameter라고 한다.

이 Hyper Parameter들이 학습시간과 학습 정확도에 어떠한 영향을 미칠지는 직접 시도를 해봐야 한다.

그래서 일반적인 모델의 구현 순서는 Idea -> Code -> Experiment -> Idea ..의 반복이라고 할 수있다.

요즈음에는 이러한 Hyper Parameter의 값을 자동으로 튜닝해주는 AutoML 분야의 리서치가 활발하게 이루어 지고 있는것 같으니 관련 자료를 찾아보면 좋을 것 같다.

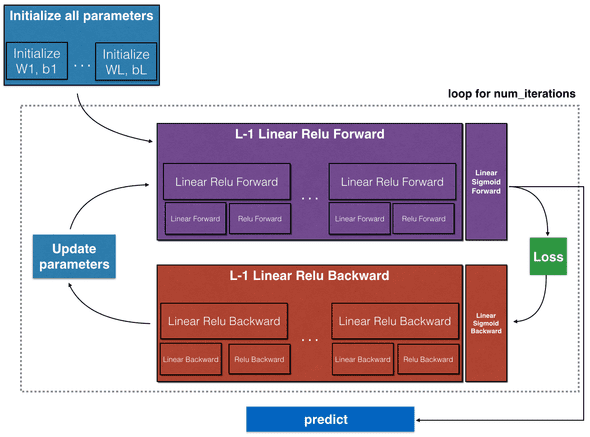
Model outline

Model Implementation

Import packages

필요한 라이브러리들을 import해준다.

sigmoid,relu와 그에 따른 미분값을 반환해주는 함수는 직접 구현하지 않았다.

import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases import *
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
from public_tests import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

initialize parameters

propagation에 필요한 초기 parameter들을 초기화 시켜준다. deep neural network이기 때문에 0이 아닌 random값으로 초기화 해주어야 한다.

def initialize_parameters_deep(layer_dims):

    parameters = {}
    L = len(layer_dims) # number of layers in the network  

    for l in range(1, L):

        parameters['W'+str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
        parameters['b'+str(l)] = np.zeros((layer_dims[l],1))
              
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

        
    return parameters

linear forward

Z를 계산하여 return해준다. Activation function까지 계산하지 않는것은, 추후 relu 와 sigmoid의 두가지 종류를 사용하기 때문에 호환성을 위해 분리한다.

계산값 Z와 A,W,b가 담겨있는 cache를 return

def linear_forward(A, W, b):

    Z=W.dot(A)+b
    
    cache = (A, W, b)
    
    return Z, cache

linearactivationforward

sigmoid, relu 에 맞게 계산하여 return

def linear_activation_forward(A_prev, W, b, activation):

    
    if activation == "sigmoid":

        Z,linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = sigmoid(Z)

    
    elif activation == "relu":

        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = relu(Z)
        

    cache = (linear_cache, activation_cache)

    return A, cache

Layer model forward

1~L번째 레이어까지 forward propagation을 진행한다.

1-L-1번째 까지는 relu를 사용하고, L번째 레이어는 sigmoid를 사용해 결과를 도출한다.

def L_model_forward(X, parameters):


    caches = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network

    for l in range(1, L):
        A_prev = A 

        W=parameters['W'+str(l)]
        b=parameters['b'+str(l)]
        A,cache = linear_activation_forward(A_prev,W,b,'relu')
        caches.append(cache)
        
    W=parameters['W'+str(L)]
    b=parameters['b'+str(L)]
    AL,cache= linear_activation_forward(A,W,b,'sigmoid')
    caches.append(cache)
    
        
    return AL, caches

Cost function

forward propagation을 마친 최종 A값으로 cost를 계산한다.

def compute_cost(AL, Y):

    
    m = Y.shape[1]

    cost = (-1/m)*np.sum((Y*(np.log(AL)))+(1-Y)*(np.log(1-AL)))

    cost = np.squeeze(cost)    #np array to real number

    
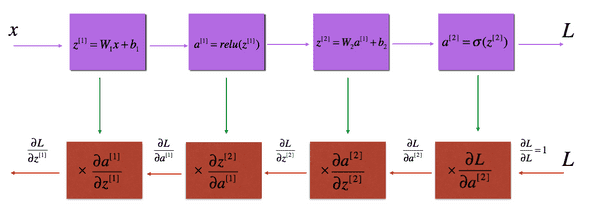
    return cost

Backward propagation

back propagation도 마찬가지로 linear 부분은 따로 함수로 빼어 재사용 한다.

linear backprop

def linear_backward(dZ, cache):

    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = (1/m) * dZ.dot(A_prev.T)
    db = (1/m) * np.sum(dZ,keepdims=True,axis=1)
    dA_prev = W.T.dot(dZ) #틀렸던 부분. dW가아니라 W
    
    
    return dA_prev, dW, db

activation backprop

def linear_activation_backward(dA, cache, activation):

    linear_cache, activation_cache = cache
    
    if activation == "relu":

        dZ = relu_backward(dA,activation_cache)
        dA_prev, dW, db = linear_backward(dZ,linear_cache)
        

        
    elif activation == "sigmoid":

        dZ =sigmoid_backward(dA,activation_cache)
        dA_prev, dW, db = linear_backward(dZ,linear_cache)
 
    
    return dA_prev, dW, db

Layer backward propagation

L은 sigmoid backward, L-1~0번째는 relu로 backprop진행한다. (code에서 인덱스 주의)

def L_model_backward(AL, Y, caches):

    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL

    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
    

    current_cache = caches[L-1]
    dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dAL,current_cache,'sigmoid')
    grads['dA'+str(L-1)] =dA_prev_temp
    grads['dW'+str(L)]=dW_temp
    grads['db'+str(L)]=db_temp

    
    # Loop from l=L-2 to l=0
    for l in reversed(range(L-1)):

        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dA_prev_temp,current_cache,'relu')
        grads['dA'+str(l)] =dA_prev_temp
        grads['dW'+str(l+1)]=dW_temp
        grads['db'+str(l+1)]=db_temp

    return grads

Update Parameters

def update_parameters(params, grads, learning_rate):

    parameters = params.copy()
    L = len(parameters) // 2 # number of layers in the neural network


    for l in range(L):

        parameters['W'+str(l+1)] = parameters['W'+str(l+1)] - learning_rate * grads['dW'+str(l+1)]
        parameters['b'+str(l+1)] = parameters['b'+str(l+1)] - learning_rate * grads['db'+str(l+1)]

    return parameters

연관글

Neural Networks and Deep Learning

Python and Vectorization

Logistic Regression for classify Cats

Shallow Neural Networks

Deep Neural Networks (now)