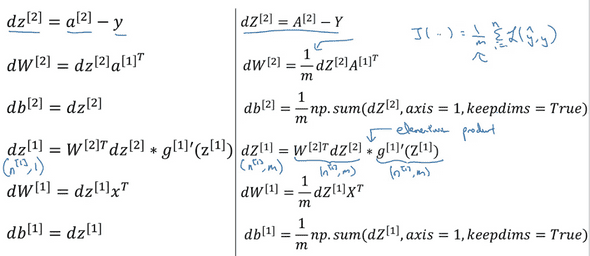Shallow Neural Networks
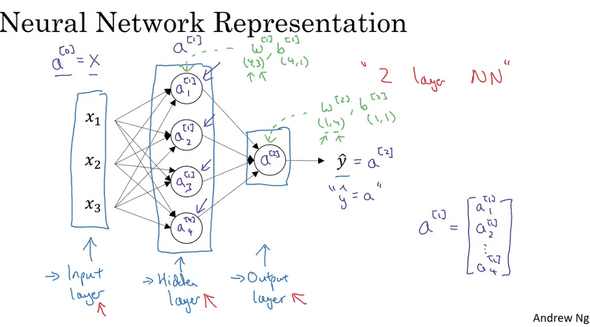
위의 그림은 2 layer neural network를 나타낸 것이다.
언뜻 보기에 층(layer)이 3개인데 왜 2 layer 라고 할까? 전통적으로, 입력 레이어는 카운트하지 않는다.
우리가 앞서 구현했던 Logistic regression 신경망에서 중간에 하나의 hidden layer를 더한 형태이다.
hidden layer는 실제로는 각 노드에 값이 존재하지만 입력,결과 레이어와 달리 우리에게 그 값이 보여지지 않는다는 의미에서 hidden layer라고 부른다.
하지만 낯선 개념은 전혀 없다고 볼 수 있다. 입력레이어로부터 hidden layer로 forward propagation을 한다. hidden layer로부터 결과 레이어까지 마찬가지로 진행한다. 그냥 같은 작업을 겹쳐놓은 것이다.
Neural Network Representation
입력 레이어로부터 나온 sigmoid 값을 a^[0]이라고 하고, 두번째(hidden layer)로부터 나온 sigmoid 값을 a^[1]이라고 한다. 여기서 조심해야할 것은, 각 레이어의 a(i)값과 잘 구별해야 한다는 것이다.
a(i)는 그 레이어의 각 노드에 대한 값이고 a^[i]는 i번째 레이어의 전체 값이다.
예를들어 a^[2] 는 2번째 층의 모든 히든 노드에 대한 a값의 집합일것이고
a^[2] ( 2 )는 2번째 층의 모든 노드의 2번째 example에 대한 값일 것이다.
그리고 a(2)^[2]는 2번째층의 2번째 노드의 모든 값이다.
또한 우리는 위의 그림을 통해서 각 레이어의 w,b의 dimension을 유추할 수 있다.
a^[1] hidden layer의 w는 (4,3)이 될것이다. 이 shape는 ''현재 레이어 단계에 4개의 노드가 있으며, 노드로 들어오는 입력값은 3개다.' 라는 의미로 해석이 가능하다.
이를 대입해보면 a^[2] 결과레이어는 (1,4)의 모양을 가진다는 것을 알 수 있다.
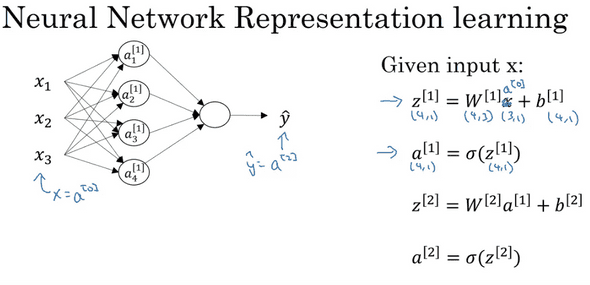
우리가 해왔던 거랑 마찬가지로, multi layer에서도 각 layer의 값들을 묶어 vectorization 할 수 있고, vector matrix단위로 연산 또한 할 수 있다.
Vectorizing Across Multiple Examples
금방 했던 과정은 Input example 한개의 데이터에 대해서 multi layer에서의 vectorization이다.
당연하겠지만 여러개의 input example에 대해서도 vectorization이 가능하다.
X는 이전에 했던것과 같이 전체 examples를 나타낸다.
Z^[1]은 1번째 layer에서의 값들인데, 각 Column은 하나의 example이고 그 각 요소는 hidden layer의 노드에 각각 들어가는 요소가 된다. 즉 Z^[ 1 ] ( i )에서 i가 노드(hidden unit)의 개수임을 알 수 있다.
마찬가지로 A에도 동일한 법칙이 적용된다. (A=sigmoid(Z)이기 때문에.)
Activation Functions
신경망에서 sigmoid 함수를 쓰는것은 항상 좋은 선택이라고는 볼 수 없다. sigmoid처럼 신경망 학습에 쓸 수 있는 많은 함수들이 있는데, 그것들을 우리는 **Activation Functions **라고 부른다.
sigmoid는 항상 0~1의 값을 return하게 해주지만, sigmoid보다 좋게 기능하는 함수들은 대부분 tangent 나 hyperbolic tangent 함수들이다.
왜냐하면 tanh 의 함수는 레이어에서 평균값이 0.5가 아니라 0에 맞춰지도록 계산되고, 이것은 다음 레이어로 하여금 조금이라도 더 쉽게 학습할 수 있게 해준다.
사실상 hidden layer에 있어서 tangent함수가 sigmoid가 대부분 우세하기 때문에 sigmoid함수를 거의 쓸 일이 없을 수 있다. 하지만 출력 레이어는 예외인데, 0~1의 값으로 나오는 것이 우리들로 하여금 binary classification을 더 쉽게 도출할 수 있게 해준다.
Activation Function의 주요 기능은 노드가 계산한 값 z가 얼마나 크던지, 얼마나 작던지 0 근처의 값으로 만들어 주어서 gradient descent를 할 때 경사를 적당히 조절해 주는 역할을 한다.
machine learning에서의 또다른 인기있는 선택지는 rectified linear unit 이 있다. 그중 ReLU function을 보자면
그래프를 보면 알 수 있듯이, 0보다 클때는 기울기가 항상 1이고, 작을때는 항상 0이다. 값이 0일때 기울기 정의가 잘 잘 안된다는 문제가 있지만, 실제 컴퓨팅 계산에서 값이 정확히 0이 나오는 경우는 매우 드물어서 걱정하지 않아도 된다.
ReLU에서는 값이 음수면 항상 0의 기울기를 가지는데, 이것은 대체로 학습에 있어서 잘 작동하지만 아닐때도 있다. 따라서 음수을때 아주 작은 기울기를 주는 Leaky ReLU 라는것이 존재한다. (하지만 잘 쓰지 않음)
신경망의 학습에 있어서 우리는 히든 레이어와 유닛의 개수, 무슨 activation function을 사용해야할지 선택지가 많다. 어떤 데이터와 신경망에 있어 무엇을 써야한다는 아직까지 명확하게 수립된 법칙은 없다. 따라서 이러한 hyper parameter들을 잘 조정하고 결정하는것이 중요하다.
그렇다면 이 Activation function은 왜 써야할까? 만약 Activation Function을 쓰지 않을 경우 어떻게 되는걸까?
실제로 activation function을 사용하는 과정을 빼고 신경망을 학습시켜보면, 노드는 그저 x에 대한 linear 한 계산만 해서 다음 레이어로 넘기는것을 반복할 뿐이다. 이렇게 되면 신경망이 많은 hidden layer를 가지고 있는것이 소용이 없게 된다.
Gradient Descent for Neural Networks
각 activation function들의 미분은 아래와 같이 구할 수 있다. 증명
sigmoid g'(z) = a(1-a)
tanh g'(z) = 1-(tanh(z))^2
ReLU g'(z) = { 1 if z > 0, 0 if z <0 }
위의 값들을 이용하여 우리는 Neural Network에서의 Back propagation또한 아래와 같이 계산할 수 있다.
Random Initialization
앞서 구현한 Logistic regression에서는 parameters를 0으로 초기화 해도 괜찮았지만, 여러개의 layer가 있는 neural network에서는 치명적이다.
만약 weights를 0으로 초기화 할 시, 학습을 계속 진행해도 레이어 안의 히든 유닛들은 똑같은 값을 산출해낼 것이고 아무리 반복해도 히든 유닛들은 완전히 똑같은 함수를 결과로 낸다.
이것은 히든 유닛의 존재 의미 자체를 없애버리기 때문에 weight를 0으로 초기화하면 안된다.
따라서, 우리는 weight 들을 random하게 설정해주어야 한다.
보통 이러한 random값은 0.01등과 같은 아주 작은 값으로 설정하는데, 그 이유는 조금만 생각해보면 알 수 있다.
우리가 앞서 봤던 tanh activation 함수들, sigmoid같은 함수들은 값이 크면 기울기가 0에 수렴한다.
이는 곧 gradient descent가 매우 느리게 적용되며, 학습시간 자체도 매우 지연될 것이다.
0.01과 같은 적절한 weight값을 정하는 방법은 다음 시간에 자세히 다뤄보도록 한다.
연관글
Neural Networks and Deep Learning
Logistic Regression for classify Cats
Shallow Neural Networks (Now)