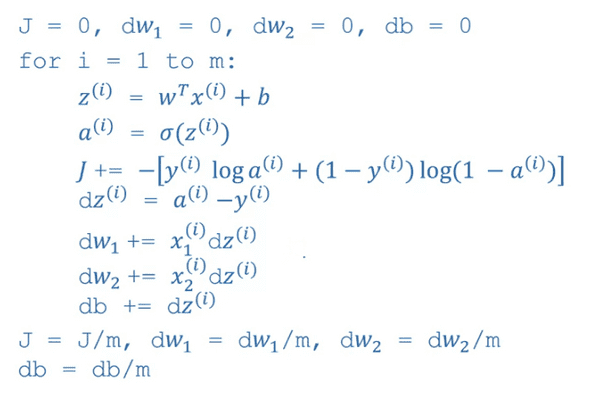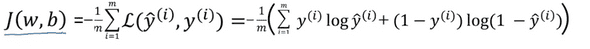Python and Vectorization
저번 글에 이어 이번에는 딥러닝을 실제로 코드로 구현하는데에 있어 중요한 개념인 Vectorization에 대해서 얘기한다.
Deep learning은 대부분 Big data를 학습하기 때문에 for문을 없애고 데이터를 vectorization하는 것은 학습 속도에 있어서 매우 중요한 요인이다.
Vectorization
앞서 말한 것 처럼 Vectorization과정은 매우 중요하다.
이 Vectorization을 하기위해 우리는 Python library인 Numpy 를 사용하여 직접 벡터연산을 할 수 있다.
a = np.random.rand(1000000)
b = np.random.rand(1000000)
#100만개의 랜덤원소 어레이 생성
c = np.dot(a,b)
#직접 벡터연산
for i in range(1000000):
c += a[i]*b[i]
#반복문으로 연산위처럼 직접 벡터연산을 하는것이랑 반복문을 통한 연산은 컴퓨터 성능에 따라 차이가 있겠지만 수백배 정도의 차이까지 난다.
이러한 CPU나 GPU의 Parallelization instruction(SIMD:Single Instruction Multiple Data)을 지원하고, python의 numpy가 이것을 활용할 수 있게 계산을 빨리하도록 처리해준다.
다른 예로 만약 v=[v1...vn]의 벡터를 exponential한 u라는 벡터를 만든다고 생각해보자.
for 반복문을 이용한다면
u = np.zeros((n,1))
for i in range(n):
u[i]=math.exp(v[i])가될것이다. 하지만 numpy의 내장함수를 이용하면
u=np.exp(v)한줄로 해결이 가능하며, 연산 속도도 훨씬 빠르다.
이 밖에도 np.log(), np.abs(), np.maximum(), 등등 다양한 내장함수를 사용하여 explicit for loop를 없앨 수 있다.
Vectorizing Logistic Regression
우리가 Logistic Regression에서 A = sigmoid(Z) 를 구하는 식을 다시 떠올려보면
z(i) = w.t * x(i) +b 가되고 전체의 dataset X에 대하여는
Z = [z(1) + z(2) + ... + z(n)] = w.t * X + b 가 될 것이다.
각각의 z에 대하여 계산하고 합쳐 Z를 만드는것 보다는, Z= np.dot(w.t * X) + b로 한번에 해결이 가능하다.
여기서 b는 원래 real number지만, numpy는 이렇게 vector matrix 연산에 쓰일 경우 자동으로 연산되는 vector matrix의 크기(1xm)로 확장하여 연산을 한다. 그리고 이것을 'Broadcasting' 이라고 한다.
마찬가지로 gradient를 구할 때도 마찬가지다
dZ = [dz(1), dz(2), ... , dz(m)]를 구할때도
A = [a(1)...a(m)] 과 Y = [y(1)...y(m)]에 대하여 dZ = A - Y 를 실행하면 바로 도출할 수 있다.
이후 dw, db도 1/m * X * dz.t , 1/m * np.sum(dz)를 구해주면 된다.
dw에서 dz를 transpose하는 이유는 X는 각 데이터가 세로로 나열되어있는 nx * m 의 형태이고, dz는 1 * m의 형태이기 때문에 원하는 값을 얻으려면 transpose 해준 후 곱해야 한다.
back propagation에 있어서 for loop를 사용한것과 제외한것을 비교해보면
에서
import numpy as np
Z= np.dot(w.t,X) + b
A = sigmoid(Z)
dZ = A - Y
dw = 1/m * dz.t
db = 1/m * np.sum(dz)
w = w-a*dw
b = b-a*db로 만들 수 있다.
A Note on Python/Numpy Vectors
numpy는 broadcasting과 같이 편리하고 강력한 기능을 제공해주기도 하지만, 반대로 그에 따른 잡기 힘든 버그나 에러를 뱉어낼 수도 있다.
그래서 간단하게 python/numpy를 이용하여 vector를 만들 때 도움이 될만한 내용을 소개한다.
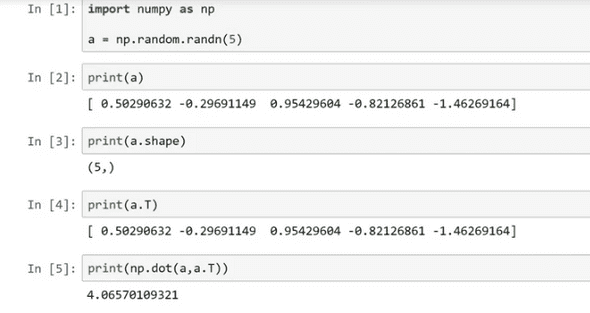
위에서 생성된 가우시안 랜덤값 5개를 같는 vector의 모양은 a.shape() 함수를 통해 (5, ) 라는 것을 알 수 있다.
이같은 모양을 rank1 vector라고 부르는데, 상당히 애매하다.
예를들어 a.T를 통해 transpose해도 예상과 달리 5x1의 matrix가 나오지 않고, np.dot(a,a.T)를해도 matrix가 나오지 않는다.
따라서 우리는 matrix를 생성할 때 a = np.random.randn(5,1) 처럼 미리 shape를 지정해줄 수 있다.
그러면 우리가 원했던 것처럼 5x1의 세로벡터가 나온다. 마찬가지로 a.T 를하면 1x5의 matrix가 반환된다.
이처럼 array를 만들 때 rank1 array보다는 row vector나 column vector를 생성하면 우리가 생각하는 연산의 결과를 낼 때 더욱 편할것이다.
그리고 vector 의 dimension이 파악이 안 될 경우 assert(a.shape==(5,1))과 같이 assert안에 넣어주면, 자신이 원하는 dimension이 아닐 경우 파이썬에서 error를 반환해 준다.
Explanation of Logistic Regression Cost Function
우리가 Logistic Regression에서 Cost function을 최소화 해야 한다고 배웠다.
그러면 왜 Cost function을 최소화 하여야하고, 어떠한 함수를 쓰는지에 대해서 간략히 알아본다.
각각의 입력값 x에 대하여 우리는 yhat을 구하는데, yhat = p(y=1 | x ) 라고 배웠다. (x값에 대해 y가 1일 확률)
만약 y = 1이라면 p(y|x) = yhat이고 , y=0이라면 p(y|x) = 1-yhat이되는데,
p(y | x) = yhat^y * (1-yhat)^(1-y)의 식에 y=1과 y=0을 넣어보면 왜 그런지 직관적으로 이해할 수 있다.
여기에 단조 증가 함수인 log를 취하면 앞서 배운 Loss function인 y * logy_hat + (1-y) * log(1-y^hat)이 나온다.
log p(x|y) = - L(y_hat,y) 에서 Loss를 최소화 시키는것은 Log를 최대화 시키는 것이기 때문에 -부호를 붙여준다.
Cost function은 Loss function의 합이며, Cost를 최소화 하는 확률을 구해야 하기 때문에 -부호를 넣어 양수로 상쇄시켜주면
J(w,b) = 1/m * sigma i=1 to m * L( y_hat(i), y(i) ) 라는 식이 도출된다.
연관글
Neural Networks and Deep Learning
Python and Vectorization (now)