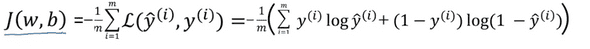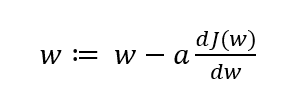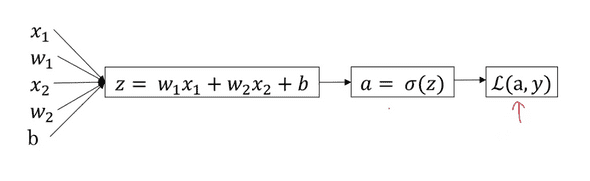Neural Networks and Deep Learning
Deep Learning의 시작에 있어서 가장 기초적인 지식에 대해서 다룬다.
Logistic regression에 대한 기본 개념을 다룬 후, 그에 필요한 여러가지 함수들과
함수의 값을 최소로 만들기 위한 Gradient Descent, 이를 위한 함수의 parameter를 조절하는 Propagation에 대한 내용을 포함한다.
Binary Classification
Binary Classification은 어떤 문제에 대하여 답이 1(true) 혹은 0(false)로 나뉘어 질 수 있는 경우를 말한다.
대표적인 예로 고양이의 Image를 주고 고양이인지(1) 아닌지(0) 판별하는 문제를 생각할 수 있다.
만약 고양이 사진을 데이터로 표현한다면 흑백이라면 1개, 컬러라면 R, G, B의 3개의 레이어에 사진의 크기 (i*j)만큼의 값이 들어있을 것이다.
이러한 데이터를 입력벡터로 나타내면 와 같은 모양이 나올것이다.
M은 위의 데이터를 여러개 모아둔 traing examples라고 볼 수 있다. M의 요소는 (X,y)의 쌍으로 나타낼 수 있고 X는 위에서 말한 사진의 데이터, y는 그것에 대한 답이다.
이 M을 일정한 비율로 Mtrain, Mtest로 나눌 수 있고 Mtrain은 모델을 학습시키는데, Mtest는 성능을 평가하는데 사용한다.
X = [x1+x2+...+xn]까지의 집합이고 X= nx*m 차원의 shape를 가진다. (data)
y=[y1+y2+...+yn]까지의 집합이고 Y=1*m차원의 shape를 가진다. (labels)
위의 표현들은 deep learning programming에 있어서 convention 같은 변수명이다.
Logistic Regression
Logistic Regression은 앞서 말한 Binary classification 에 사용될 수 있다.
주어진 X에 대하여 우리는 y_hat을 구하길 원한다.
y_hat은 앞의 예제에서 X라는 사진이 주어지면 그 사진이 고양이일 확률은 얼마나 되는가? 를 표현한다.
이 y_hat을 구하기위해 Logistic Regression을 사용하고 그 parameter인 w와 (X와같은차원,) b(real number)를 사용하여 식을 표현할 수 있다.
y_hat = w.transpose * x + b
하지만 위의 식은 Binary classification에는 적합하지않은데, 왜냐하면 도출되는 범위가 1보다 크거나 음수일 수 있기 때문이다.
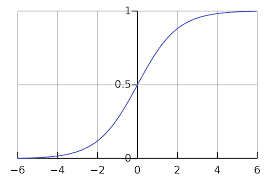
따라서 확률로 표현하기 적합한 0~1의 범위를 가지는 sigmoid함수로 감싸주어 완성한다.
(감싸주는 함수는 activation function이라 부르고 여러가지가 있으며, 저마다의 특성을 가지고있다. 우선은 sigmoid를 예로 들었다.)
즉 Logistic regression을 사용하면 신경망을 통해 y_hat을 실제 y에 가깝도록 예측할 수 있는 w,b를 학습하는 것이다.
Loss Function
그리고 우리는 만들어낸 y_hat이 실제 y에 얼마나 가까운지를 측정하기위해 Loss function을 쓴다.
Loss function은 1/2 * (y_hat-y)^2 의 squared error로 표현할 수 있지만, 해당 식을 쓸 경우 우리는 여러개의 local optima가 생기는 non convex 곡선이 생기기 때문에 optimization problem이 생긴다.
따라서 squared error와 비슷한 역할을 하지만 다른 식을 쓰도록 한다.
그 식은 L(yhat,y) = -(ylogyhat + (1-y)log(1-y_hat)) 이다.
위의 식은 y에 1과 0을 대입해보면 사용의 타당성을 입증할 수 있다.
1을 넣으면 L = -log yhat이 나오고, 따라서 Loss function의 값을 작게만드려면 -log yhat을 크게 만들어야하니 y_hat또한 커져야한다.
반대로 0을 넣으면 L=-log(1-yhat)이고 이 값을 작게만드려면 yhat이 작아져야하기 때문에 y_hat은 y를 따라가려는 속성을 보인다.
Cost Function
Cost function은 각각의 y에 대한 식인 Loss function과 달리 traianing examples 전체에 대해 어떻게 진행되고 있는지를 판단하는 척도이다.
식에서 볼 수 있듯이 Cost function은 Lost function들의 평균이라고 볼 수 있다.
우리는 cost fucntion J를 작게 만들 수 있는 w, b 를 찾아야 한다.
Gradient descent
Cost function J의 값을 w,b평면에 대해 나타내면 다음과 같다.
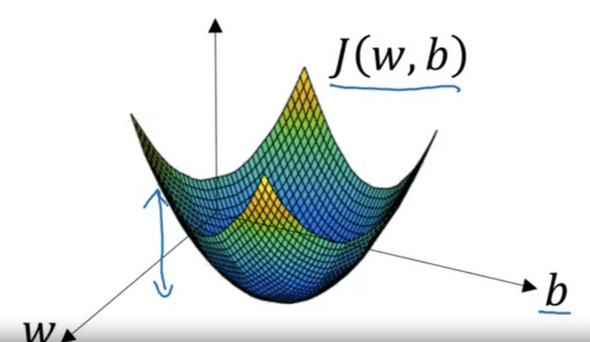
앞서 말했듯이 우리가 해야할 것은 J 의값이 최저가되는 W,b의 값을 찾는것이다. Cost function은 Convex 하기 때문에 최저 지점을 찾을 수 있다.
어떠한 J의 위치에서, Gradient Descent의 과정을 반복하면 결국 Convex의 최저값으로 수렴하게 되어있다.
이 과정을 수식화하면
이고, 각 반복마다 수행한다. (여기서 a는 learning rate이고, 추후에 자세히 설명한다.)
반복을 할수록, w에 대해 미분함에 따라 점차 convex의 global optimum에 수렴하게 된다. (b에 대해서도 동일하게 수행)
Computation Graph
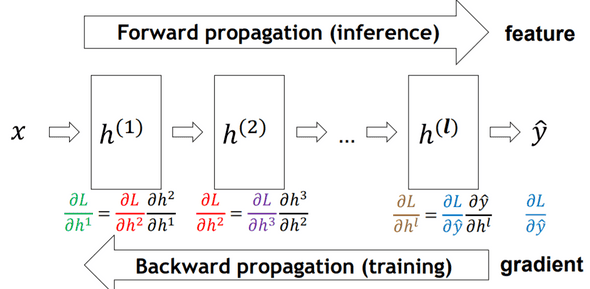
우리는 신경망을 학습할 때 순전파(foward propagation) 역전파(Back propagation) 과정을 거친다.
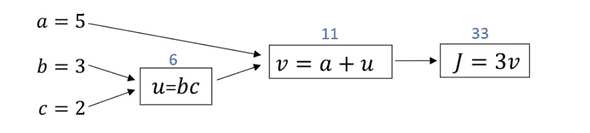
f(a,b,c) =3(a+bc) 라는 식을 Computing graph로 나타내면 위와 같다.
만약 a를 0.001증가시킨다면 v또한 0.001이 증가하게될것이고, J는 0.003이 커진다.
이처럼 a가 변하면 a->v->J 를거쳐 영향이 나타나게 되는데, 이 성질을 이용한 Chain rule으로 인해
dv/da * dJ/dv = dJ/da가 성립한다. dJ/du = dJ/dv * dv/du도 마찬가지로 성립하고,
위의 식에서 구한값들을 이용해 dJ/db도 아래처럼 구할 수 있다.
dJ/db = dJ/du * du/db
즉, dJ/du를 한번 구해놓으면 dJ/da, dJ/db, dJ/dc를 구하는데 모두 사용할 수 있다.
Logistic Regression Gradient descent
x1,x2의 vector가 입력되고 그에 따른 w1,w2 그리고 b가 있다.
위의 사진에 대해서 Back propagation을 시행하면 da = dL(a,y)/da, dz= da/dz * dL(a,y)/da = a-y이다. (왜 a-y인지는 미분)
해당 값들로 dL/dw1 = x1 * dz , dL/dw2 = x2 * dz, db=dz를 도출할 수 있다.
그 후 w1= w1-a * dw1, w2= w2 - a * dw2, b = b-a * db로 update 할 수 있다.
위의 과정이 training example 하나에 대해서 back propagation으로 값을 업데이트 한 과정이다.
그렇다면 M개의 training examples에 대해서는 어떻게 계산할까?
마찬가지로 각각의 원소에 대해 derivative를 구하면서 합치고, 마지막에 M의 크기로 나누어 주면 된다.
그러면 전체 M에 대한 w1, w2, b를 구할 수 있다.
이때, 그림처럼 x1,x처럼 2개의 특징 벡터가 존재할 때와 달리, 여러개의 특징이 존재한다면 그것만큼 반복을 해서 구해줘야한다.
하지만 Deep learning에서 학습시키는 데이터셋은 갈수록 커지고 있기 때문에 이러한 for 문을 코드에서 없애는 것이 매우매우 중요하다. 이러한 과정을 vectorization이라고 하고, 다음 글에서 다룬다.
연관글
Neural Networks and Deep Learning (now)