MIRNet

https://arxiv.org/pdf/2003.06792.pdf https://github.com/swz30/MIRNet

Method

Image enhancement에 있어서, 기존의 방법론들은 아래와 같은 장단점이 존재한다.

full-resolution (single resolution)

• spatially precise, contextually less robust

progressively (encoder-decoder)

• semantically reliable, spatially less accurate
• broad context learning, 하지만 low stage 단계에서 spatial detail이 손실되고 복구되기 매우 어렵다.

때문에 저자는 high resolution에서의 spatiality , low resolution에서의 contextual information을 parallel convolution stream 을 통해서 동시에 보존하는 방법을 제시한다.

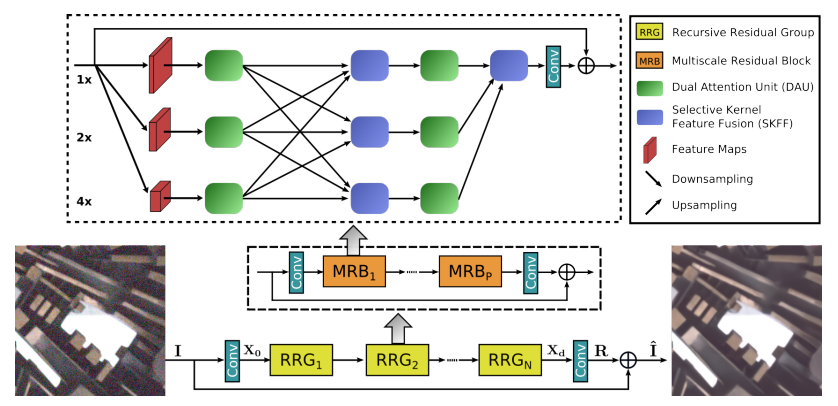
MIRNet 은 기존의 multi scale approach 와 비교하여 다음과 같은 특성을 갖는다.

• Single-Resolution에 대해 Spatial, Channel attention을 수행한다. (DAU)
• Parallel convolution stream에서 모든 resolution 간의 information exchange 를 수행한다.
• 각 resolution의 feature들을 그냥 합치는 것이 아니라, self attention base의 selective kernel method를 통해서 fuse 하여 유효한 feature를 selective하게 뽑아낸다. (SKFF)
• recursive residual design을 통해 정보 손실을 최소화 하며 deep network 구성 가능하다.
• residual resizing module을 통해 정보 손실을 최소하 하여 Down/Up sample을 실행한다.

Components

MRB

MRB (Multiscale Residual Block)

MIRNet은 MRB에 대한 RRG(Recursive Residual Group) 으로 구성 되어있으며,

MRB는 다음과 같은 구성요소들을 포함하고 있다.

1. Residual Resizing module
2. Dual Attention Unit (DAU)
3. Selective Kernel Feature Fusion (SKFF)

1. Residual resizing

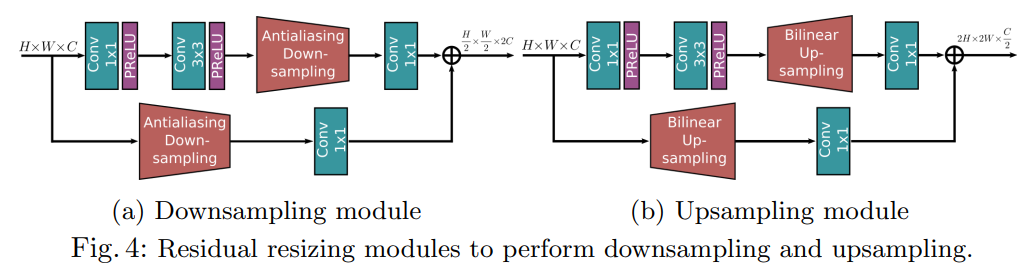
각 MRB 에 대해 recursive residual 구조를 적용하기 위해서는 Input과 output tensor의 크기가 Constant해야한다.

이를 위해 Down sample, Up sample의 resizing 과정이 존재하는데, 저자는 이 과정에서 정보 손실을 최소화 하기 위해

1. Residual resizing
2. Anti-aliasing down sampling

을 적용하였다.

Down sample은 H/2 x W/2 x 2C,

Up sample은 2H x 2W x C/2 의 결과가 나오게 되고,

논문에서는 해당 모듈을 연속적으로 적용시켜 X2, X4 의 resolution을 얻어낸다. (Up sample도 마찬가지)

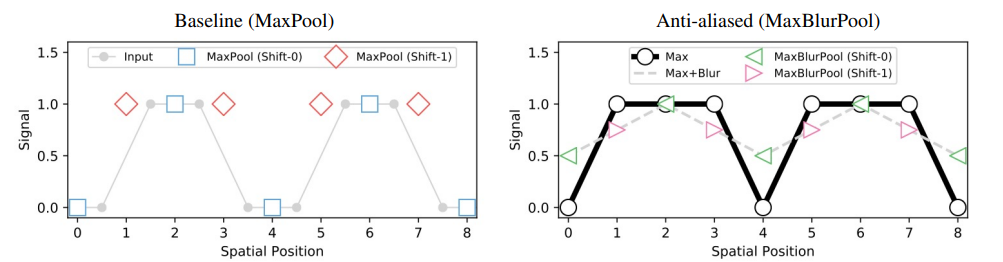
Anti-aliasing down sampling은 Conv layer가 shift-variance를 방지하기 위해 shift-equivariance/invariance 를 증진시키기 위한 방법이다.

해당 논문에서는 Max Pool 과 Blur Pool 의 장점을 둘 다 취할 수 있는 방법을 소개하는데, 효과가 있는지는 잘 모르겠다.

Ref

Anti-aliasing downsampling: Making convolutional networks shift-invariant again. In: ICML (2019) http://proceedings.mlr.press/v97/zhang19a/zhang19a.pdf

2. DAU

Residual Resizing module 을 통해 multi-resolution에 대한 Input이 생성되면, 각각의 Input $L_n$은 DAU 를 통과하게 된다.

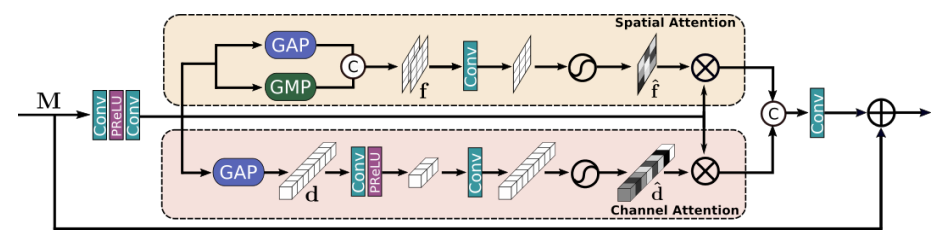
DAU(Double attention unit) 에서는 Spatial attention, Channel attention 을 통해 나온 정보들을 합쳐 feature tensor 안에서의 정보를 효과적으로 추출한다.

DAU에서는

Channel attention은 Squeeze and excitation,

Spatial attention은 CBAM의 구조를 차용하여 사용하고 있다.

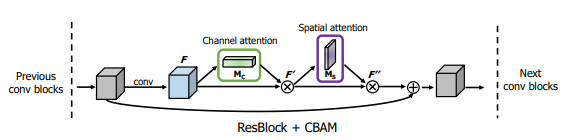
(+ CBAM 에서는 Spatial, Channel attention 둘 다 Average Pooling 뿐 만 아니라 Max Pooling 또한 중요한 정보를 잡아낼 수 있고, 각각 쓰는 것 보다 성능이 좋다고 같이 사용한다.)

DAU는 다음 과정을 수행한다.

• Input M 을 3x3 Conv + PReLU + 3x3 Conv 를 통과시킨다.
• 위의 결과를 Spatial, Channel attention unit에 통과시킨 후 각각 다시 곱해준다.
• 마지막으로 1x1 Conv를 통과시킨 후 , Input M 과 sum 해준다.

Ref

Channel attention : Squeeze-and-excitation networks. In: CVPR (2018) https://arxiv.org/pdf/1709.01507.pdf

Channel - Spatial attention: CBAM: Convolutional block attention module. In: ECCV https://arxiv.org/pdf/1807.06521.pdf

3. SKFF

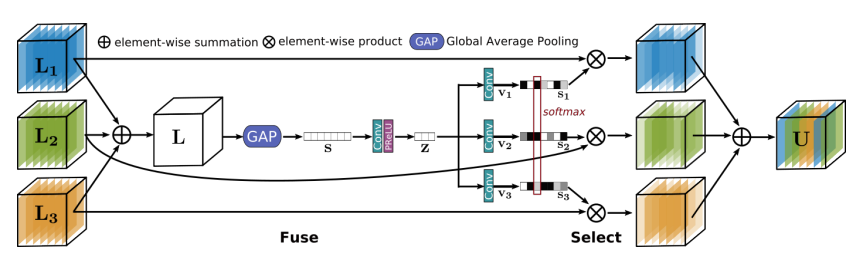
DAU를 통해 추출된 multi-resolution의 정보들은, SKFF(Selective Kernel Feature Fusion) 모듈을 통과한다.

SKFF 를 통과하며 multi-resolution 사이의 정보 교환을 통해 유효한 feature 들을 잘 추출할 수 있을 뿐 만 아니라, 단순히 concatenate 하는 것 보다 parameter 수 또한 획기적으로 줄일 수 있다.

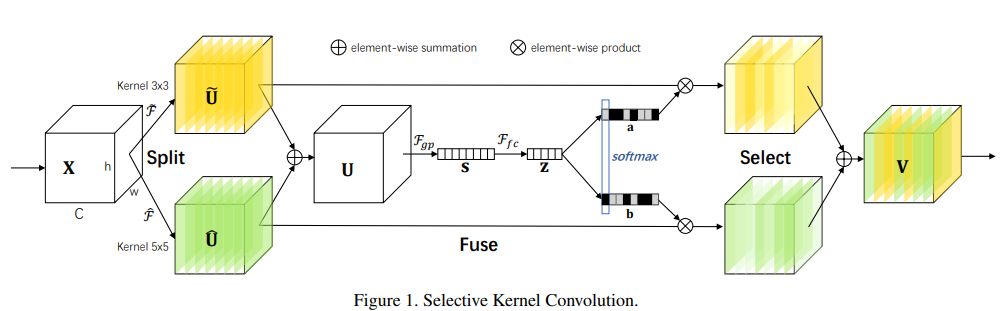
• self-attention : Selective kernel networks. In: CVPR (2019) https://arxiv.org/pdf/1903.06586.pdf

SKFF는 위 논문의 self-attention mechanism 에서 아이디어를 가져와 매우 유사하게 사용한다.

SKFF의 과정은 아래와 같다. (1~5 = Fuse, 6~7 = Select)

1. multi-resolution feature input ($L_n$)에 대해서 self attention을 하여 L 을 얻는다.
2. Global Max Pooling 을 적용한다 (1x1xC)
3. 1x1conv - ReLU 를 통해 S -> z 로의 compact feature 를 만든다. (1x1xC -> 1x1xC/8)
4. 원래 채널 수 만큼 channel upscaling conv (-> 1x1xC)
5. input layer $L_n$ 개수만큼 softmax를 취한다.
6. attention activate $s_n$과 input $L_n$ product
7. sum -> U

베이스가 되는 Selective kernel에 대해 1. multi-kernel feature 대신 multi-resolution feature 가 Fuse된다는 점, 2. s->z 의 compact feature를 만들 때 Fully connected layer 대신 1x1 Conv -> ReLU 가 사용된다는 점에서 차이가 있다.

Overall Pipeline

앞서 설명하였듯 MIRNet은 MRB에 대한 Residual Block이 RRG를 구성하고, RRG 들에 대한 Residual (skip connection) 구조로 전체 Flow가 구성된다.

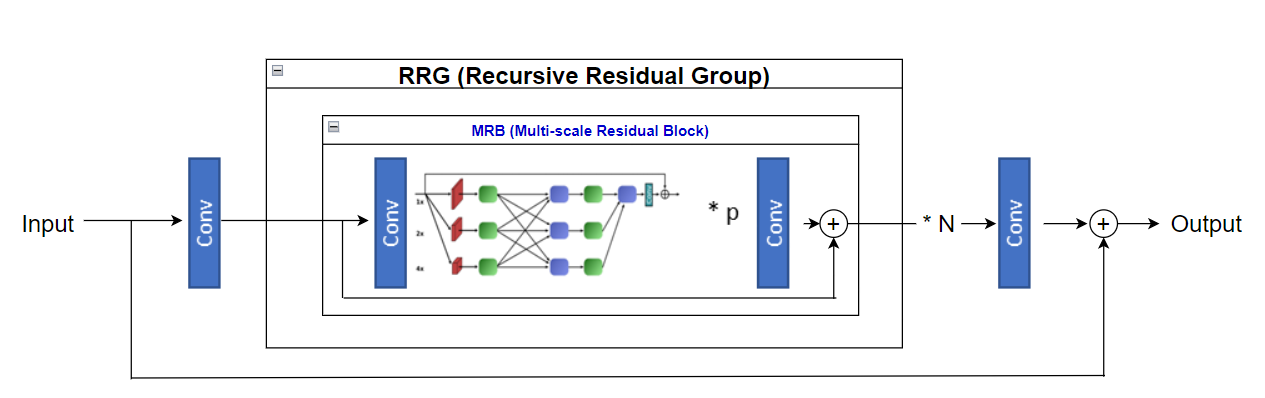
Extra refs

Denoising

traditional - transform coefficients

• Local adaptive image restoration and enhancement with the use of DFT and DCT in a running window. In: Wavelet Applications in Signal and Image Processing IV (1996)
• Noise removal via bayesian wavelet coring. In: ICIP (1996)
• De-noising by soft-thresholding. Trans. on information theory (1995)

traditional - algorithm

• Image denoising by sparse 3-D transform-domain collaborative filtering. TIP
• A non-local algorithm for image denoising. In: CVPR (2005)

Deep Learning

• Image denoising: Can plain neural networks compete with BM3D? In: CVPR (2012)
• Real image denoising with feature attention. ICCV (2019)
• Unprocessing images for learned raw denoising. In: CVPR (2019)
• Deep joint demosaicking and denoising. TOG (2016)
• Toward convolutional blind denoising of real photographs. In: CVPR (2019)
• Neural nearest neighbors networks. In: NeurIPS (2018)
• Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. TIP (2017)
• CycleISP: Real image restoration via improved data synthesis. In: CVPR (2020)
• FFDNet: Toward a fast and flexible solution for CNN-based image denoising. TIP (2018)

Super resolution

**attention base **

• Image super-resolution using very deep residual channel attention networks. In: ECCV (2018)
• Residual non-local attention networks for image restoration. In: ICLR (2019)

Enhancement

CNN

• Ntire 2019 challenge on image enhancement: Methods and results. In: CVPRW (2019)

encoder-decoder

• Low-light image enhancement via a deep hybrid network. TIP (2019)
• LLNet: a deep autoencoder approach to natural low-light image enhancement Pattern Recognition (2017)
• Encoder-decoder with atrous separable convolution for semantic image segmentation. In: ECCV (2018)