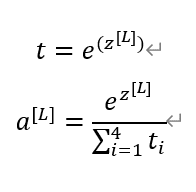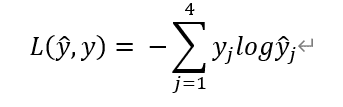Softmax Regression
우리는 이때까지 답이 1 아니면 0 즉 Binary한 문제에 대해서만 Classify를 해왔다.
하지만 그 이상의 class가 있는 경우에도 당연히 학습과 분류가 가능하고, 이를 위해 Softmax Regression을 이용한다.
위와 같이 고양이=1, 강아지=2, 병아리=3, 그외=0 의 class를 갖는 동물 분류기 모델을 만든다고 가정해보자.
우리는 결과적으로 Input에 대해 4개의 class 중 하나로 결과를 내야한다.
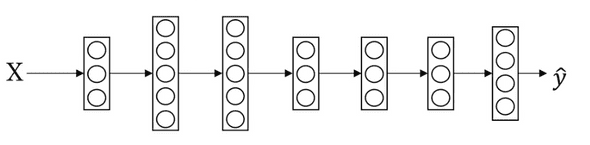
이를 위해 기존에 1개의 node만 존재하던 output layer와는 달리, class의 숫자만큼 output layer가 존재해야한다.
Forward propagation
만약 input X가 들어왔다고 하면, 마지막 Layer는 z^[L]=W^[L]a^[L]+b^[L] 의 계산으로 z를 계산하고 (4,1)의 shape를 가질 것이다.
그 후 Activation function을 거쳐 y_hat을 도출하는데, Multi class를 구별하려면 좀 다른 activation을 써야한다.
a를 도출하기 위한 임시의 t를 만들어 아래 계산을 해주면 된다.
좀 더 쉬운 이해를 위해 z^[L] 이 [5,2,-1,3] 을 갖는 (4,1) vector라고 해보자.
그러면 t = [e^5,e^2,e^-1,e^3] = [148.4,7.4,0.4,20.1] 의 (4,1)vector가 될 것이고 activation function에 넣으면
0.842, 0.042, 0.002, 0.114의 값이 나오고 이는 곧 각 Class일 확률 을 나타낸다.
Loss function & Cost function
그럼 이 activation function의 Loss function인 L(y_hat,y)는 어떻게 계산할까 ?
의 식으로 Loss 계산이 가능하다.
만약 y=[0,1,0,0] 의(4,1) vector가 있다고 했을때, 위의 식으로 Loss 를 계산하면 y1,y3,y4=0이므로 Loss 는 -log yhat2 가되고, Loss를 줄이기 위해서는 yhat2의 값을 크게 만들 수 밖에 없다.
Cost function 또한 (nx,1) 의 vector를 (nx,m)으로 확장시켜 계산하면 된다.
Gradient Descent
미분을 해보면 dz^[L] = y_hat - y 인것을 알 수 있다.
이 식을 이용해서 L ~ 1번째 까지 Back propagation을 진행하면 된다.
연관글
Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization
Practical Aspects of Deep Learning(1)