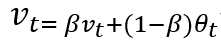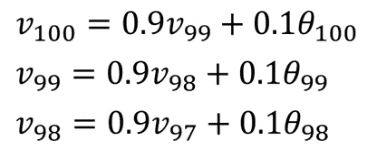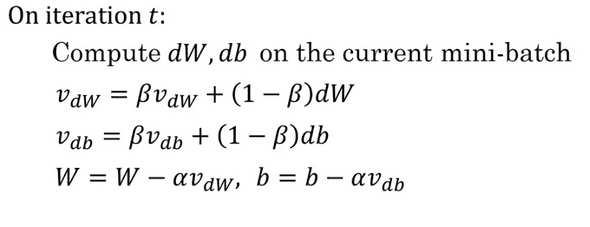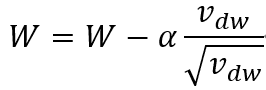Optimizing Algorithms
모델 학습에 있어서, 우리는 여러가지 Hyper Parameter를 통해 더 빠르고, 더 정확하게 데이터를 학습시킬 수 있다.
하지만 아직까지 정석적인 척도가 존재하지 않는 것이 아니라, 여러가지 환경과 경험에 의존하여 모델을 튜닝한다.
해당 글에서는 앞의 Hyper Parameter 외에도 여러가지 요소를 통해 모델을 최적화 하는 방법에 대해서 다룬다.
Mini-batch Gradient Descent
Deep learning은 일반적으로 Data의 크기가 클수록 더 잘 작동한다. 하지만 Data의 크기와 학습 시간은 반비례한다.
아무리 모델이 학습을 잘 한다고 해도, 학습시간이 엄청나게 크면 해당 모델을 유지보수 하는데에 엄청난 기회비용의 손실이 발생한다.
우리는 Data의 크기를 작게 여러개로 나누어 Gradient descent를 진행시킴으로 학습 속도를 조금 더 빠르게 할 수 있다.
Data를 일정한 개수로 나누어 묶은것을 mini-batch 라고 부른다.
예를들어 전체 Data X의 크기 m = 50,000,000 이라고 할 때, 우리는 하나의 batch당 1000개의 원소로 mini-batch 5천개로 나눌 수 있다.
여기서 새로운 notation {} 이 등장하는데, 각 mini-batch는 X^{t} 와같이 나타낸다.
전체적인 과정은 X^{t}, Y^{t}, J^{t}로 나누어 Gradient descent를 진행하는것 외에는 다른게 전혀 없다.
Epoch 는 train set 전체가 한번 통과한다는 뜻을 나타낸다.
전체 Batch로 학습시 1 epoch에 1번의 gradient descent가 일어나지만 앞의 예로 5천만을 1000 size의 mini-batch로 나눈 경우 5천번의 gradient descent가 진행된다.
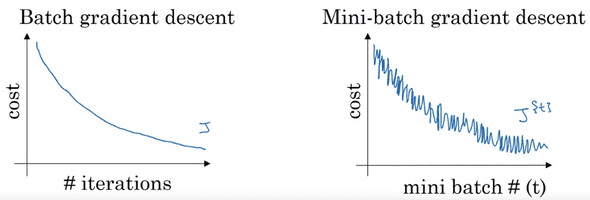
우리가 전체의 데이터셋 X에 대해 Gradient Descent를 진행할 경우, 기대되는 cost의 동향은 왼쪽과 같이 지속적으로 감소하는 모양일 것이다.
반면, 우리가 Mini-batch X^{t}에 대해 Gradient Descent를 진행할 경우, 오른쪽과 같이 들쑥 날쑥하게 감소하는 것을 볼 수 있다.
하지만 이것은 잘못된 결과가 아니다. Mini-batch의 경우, 한번의 Gradient Descent를 할 때 마다 다른 data set을 가지고 진행하는것과 같기 때문에 들쑥날쑥하게 나온다.
예를 들어 X^{1}은 학습이 쉬워서 Cost가 작게나올수도있고, X^{2}는 학습이 어려워 Cost가 높게 나올수도 있다.
Choosing mini-batch size
mini-batch 를 정하는데에는 여러가지 경우가 있다.
예를 들어 mini-batch의 사이즈를 size=m 으로 설정한다면 이는 곧 data X의 전체크기이다.
혹은 mini-batch의 사이즈를 1으로 설정한다면, gradient descent는 하나의 example마다 일어날 것이고, 이 경우를 stochastic gradient descent라고 부른다.
위의 두 extreme한 예제의 특징을 살펴보자.
Batch size의 경우 global optimum쪽으로 향하다가 점차 수렴하겠지만 Stochastic의경우 그렇지 않다.
노이즈와 함께 결국 optimum의 방향으로 가겠지만, 절대 최소값에 수렴하거나 하지는 않는다.
하지만 noise로 인해 Local optimum에 빠질 확률이 더 적어지고, 작은 단위를 계산하기 때문에 수렴 속도가 상대적으로 빠르다.
Batch size는 데이터가 클 경우 학습 속도가 매우 늘어나고, Stochastic size는 vectorization의 장점을 거의 잃기 때문에 너무 크거나 작지 않은 범위에서 적절한 사이즈를 정해야한다.
사이즈를 정하는데에 있어 약간의 가이드라인을 제시하자면 다음과 같다.
- 데이터의 규모가 작을 경우 Batch-size사용
- 데이터의 규모가 클 경우 64 - 512사이의 값 사용 (컴퓨터의 구조상 2의 지수값일때 연산이 더 빠름)
- CPU/GPU에 다 들어갈 수 있는 크기의 값 사용
Exponentially Weighted Averages
Exponentially Weighted Averages는 지수 가중 평균 이동법이라고 부른다.
전체적인 개념을 설명하자면, 어떠한 시점 t에서의 데이터는 0~t까지 모든 데이터의 가중 합으로 산출하는데, 오래된 데이터의 영향력을 지수적으로 감소시키는 방법이다.
해당 식을 B가 0.9인 어떠한 데이터에 도입하여 거꾸로 대입하여 아래 항들로 치환하면
0.1Θ(100) + 0.1*0.9Θ(99) + 0.1 * (0.9)^2Θ(98).. 과 같은 형태로 나온다.
더 오래된 항일수록 B의 지수승만큼 영향력이 급격하게 작아지는 것을 볼 수 있다.
그리고 이러한 영향은 대략 1/1-B 개의 데이터로 부터 받는다고 추측할 수 있다.
예를들어 B = 0.98이면 대략 이전 50개의 데이터에 대한 대략적인 평균치를 갖는다고 볼 수 있다.
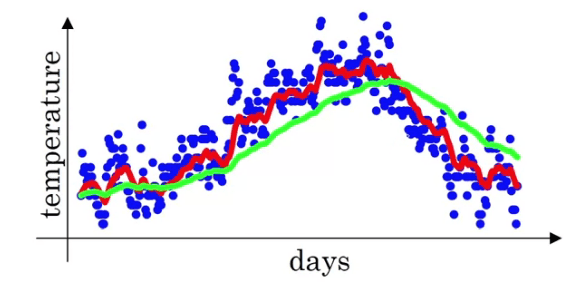
아래 그래프는 원본데이터- blue에 대해 B=0.9->red, B=0.98->green 으로 나타낸것이다.
딥러닝에 있어서 이러한 지수 가중 평균을 사용하는것은 여러가지 장점이 있다.
값의 noise를 잡아주는 효과가 있으며 또한 코드로 구현을 할 때
v=0 로 선언을 한 다음,
v=Bv + (1-B)v 로 계속 갱신시켜나가면 된다.
이처럼 단지 하나의 변수 v로 계속해서 가중합을 갱신시켜 사용하면 되므로 메모리도 많이 사용하지 않고 코드도 간결하다.
Bias correction이란 기법은 지수 가중 평균을 더 정확하게 계산할 수 있게 도와준다.
위의 그래프에서 초록색 선은 B=0.98에 대 하여 계산을 한 결과인데, 사실 위에 주어진 식으로 B=0.98을 대입하여 계산하면 초록색 선처럼 나오지 않는다.
아마 초반의 day에 대하여 예측보다 매우 낮은 부분에서 시작을 할 것이다. 이는 우리가 v를 초기화 할때 v=0으로 두기 때문에 그렇다.
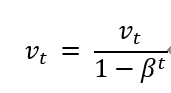
v를 위처럼 구해주면 초반 값에 대하여 bias를 correction 해주는 기능을 한다.
Gardient Descent with Momentum
Momentum의 기본적인 아이디어는 기울기의 Exponentially Weighted Average를 산출하는 것이다.
Momentum은 Gradient Descent를 가속화 시켜 전체적인 모델의 학습을 빨라지게 해준다. 그 이유는 아래와 같다.
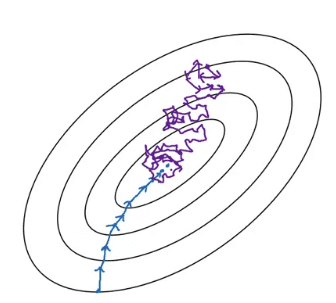
우리가 Gradient Descent를 진행할 때 파란색 선과 같이 진행된다고 생각해보자.
Optimum의 방향으로 제대로 진행되고있다는걸 알고 있기 때문에 Learning rate를 좀 더 올려 시간을 단축하고 싶지만, 그럴 경우 보라색 선과 같이 수직 방향으로 오버슈팅된다.
앞서 배운 개념인 Exponentially Weighted Average를 사용하여 이러한 현상을 막는것이 바로 Momentum이다.
Gradient를 업데이트 할 때, dW, db에 대해서 지수 가중 평균 이동을 실시한다면 몇개의 step을 진행해도 결과적으로는 크게 변함이 없는 수직방향의 영향력은 줄어들고, Optimum으로 빠르게 이동하려는 수평 방향의 영향력은 커져서 더욱 빠르게 optimum으로 도달할 수 있을 것이다.
그리고 대부분의 상황에서 B의 값은 0.9일때 잘 작동하며, 이는 이전 10개의 기울기의 평균을 참고한다고 볼 수 있다.
RMSprop
Momentum과 같이 gradient descent의 속도를 가속시킬 수 있는 기법 중 RMSprop이라는게 있다.
RMSprop은 root mean square propagation의 약자이다.
기본적인 개념은 Momentum과 매우 흡사하다. 대신 가중합을 제곱으로 유지시키고 ((1-B)dw^2), gradient를 업데이트 할 때
의 값으로 업데이트 해준다. 이는 b에 대해서도 마찬가지이다.
이해를 돕기위해 간단한 예로 db가 세로방향으로의 기울기고 dw가 가로방향으로의 기울기라고 할 때, 기울기를 업데이트 할 때 b가 상대적으로 더 큰값인 db로 나누어진 값에 대해 업데이트되기 때문에 W에 비해 영향을 덜받으며 업데이트 될 것이다.
Adam
Adam(Adaptive moment estimation)은 잘 동작할거라고 예상했던 Momentum과 RMSprop이 모든 경우에서 좋은 성능을 내지 못하자 이를 극복하고자 둘의 특성을 합쳐서 만들었다고 볼 수 있다.
그리고 Adam은 대부분의 신경망에서 잘 작동한다! 그렇기 때문에 많이 쓰인다.
Adam의 진행에 대한 pseudo code를 나타내면 아래와 같다.
v_dw=0, s_dw=0, v_db=0, s_db=0
on itertation t:
compute dw, db using gcurrent mini-batch
v_dw = B1*v_dw + (1-B1)*dw , v_db = B1*v_db + (1-B1)*db #momentum
s_dw = B2*s_dw + (1-B2)*dw^2, s_db = B2*s_db + (1-B2)*db^2 #RMSprop
v_dw_cor = v_dw/(1-B1^t) , v_db_cor = v_db/(1-B1^t)
s_dw_cor = s_dw/(1-B2^t) , s_db_cor = s_db(1-B2^t)
W:= W-a(v_dw_cor/sqrt(s_dw_cor)+epsilon)
b:= b-a(v_db_cor/sqrt(s_db_cor)+epsilon)Adam에서는 bias correction을 쓰는것이 일반적이다.
momentum과 RMSprop의 과정을 모두 구하고, W,b를 업데이트해주면 된다. 여기서 분모에 epsilon을 더해주는 것은 분모가 0에 가까운 작은값이 되면 값이 폭팔적으로 증가하기 때문에 이를 방지하기 위함이다.
Adam을 적용하는데 있어서 정해야하는 Hyper Parameter들을 정리하면 다음과 같다.
learning rate는 가장 중요한 파라미터라고 할 수 있다. 여러개의 값들을 시도해보고, 잘 학습하는 것을 고르면 된다.
B1,B2는 잘 튜닝하지 않는다. 보편적으로 B1은 0.9, B2는 0.999가 잘 작동한다고 알려져있다.
epsilon또한 잘 튜닝하지 않는데, 보통 10^-8 정도의 숫자를 사용한다.
Learning Rate Decay
천천히 Learning rate를 줄여나가는것 또한 학습 속도를 빠르게 하는데 도움이 된다. 우리는 이것을 Learning rate decay라고 부른다.
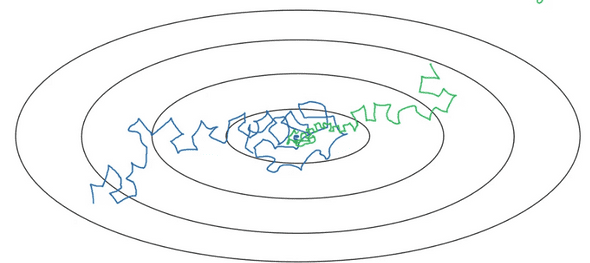
Mini-batch에서 학습을 진행할 때, 파란색과 같은 경향을 보이며 아무리 학습을 진행해도 optimum에 수렴하지는 않고 그 주변을 멤돌것이다.
반면에 학습을 해가면서 Learning rate를 줄인다면, optimum 가까이에서 noise의 영향을 덜 받아 좀 더 optimum에 가까운 범위에서 멤돌게 될 것이다.
Learning rate decay를 하는 방법에는 여러가지가 존재하고, 딱히 정답이라고 할 수 있는 것은 없다.
따라서 여러가지 방법들 중 모델이 더 나은 결과를 보이는 것을 적절히 선택해서 적용하면 되겠다.
Local Optima Problem
- 우려와는 달리, 매우 고차원에서 cost function 에서는 local optima에 갇힐 확률은 작다.
- 오히려 plateaus가 문제다. plateaus는 기울기의 값이 거의 0인 saddle point에서 빠져나가는 속도가 매우 느려지는 것을 말하는데, 앞서 배운 Adam과 같은 알고리즘이 plateaus에서 빠져나가는 속도를 크게 향상시킬 수 있다.
연관글
Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization
Practical Aspects of Deep Learning(1)