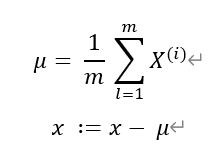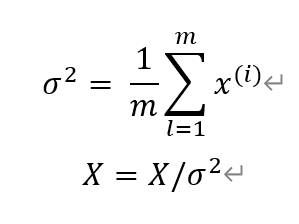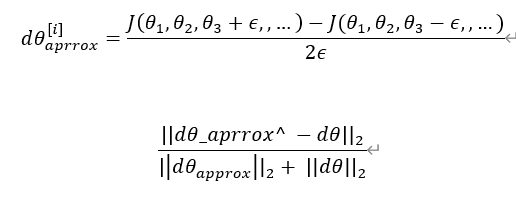Practical Aspects of Deep Learning
- Give examples of how different types of initializations can lead to different results
- Examine the importance of initialization in complex neural networks
- Explain the difference between train/dev/test sets
- Diagnose the bias and variance issues in your model
- Assess the right time and place for using regularization methods such as dropout or L2 regularization
- Explain Vanishing and Exploding gradients and how to deal with them
- Use gradient checking to verify the accuracy of your backpropagation implementation
- Apply zeros initialization, random initialization, and He initialization
- Apply regularization to a deep learning model
Setting up Optimization Problem
Normalize
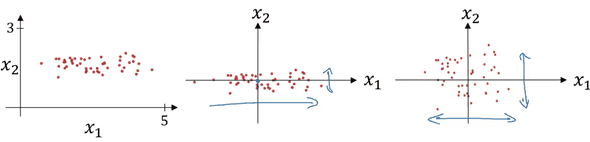
신경망 학습속도를 빠르게 하는 기술 중 하나는 인풋을 normalize하는것이다.
첫번째 그래프와 같이 분산되어 있는 input들을 최종적으로 세번째 그래프처럼 골고루 분포하게 해준다.
우선 전체 x에 대하여 평균을 빼주면 두번째 그래프와 같이 되고
그 후 위에서 구한 x에 대해 아래의 식을 수행에 전체X를 variance로 나눠주면 3번째 그래프와 같이 된다.
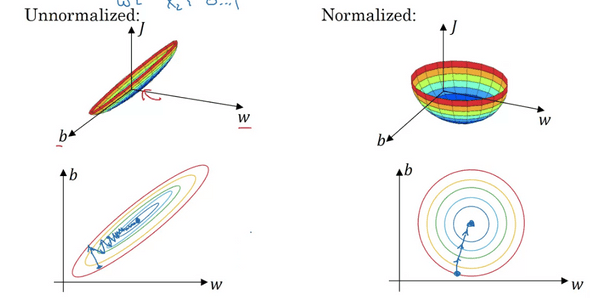
만약 x1 의 range가 1...1000과 같고 x2의 range가 0...1이면 서로 다른 variance로 인해 cost function의 그래프가 왼쪽과 같이 나올것이다.
왼쪽처럼 길쭉한 모양은 cost function이 optimum에 다가가기가 힘들고, 여러번 Gradient descent를 수행해야 한다.
반면, 오른쪽처럼 Normalize로 인해 variance가 비슷할 경우, optimum에 곧바로 향하고, 더 빠르게 수렴할 수 있다.
Vanishing / Exploding Gradients
Deep neural network의 문제점 중 하나는 신경망이 너무 깊어지면, 즉 Layer의 수가 너무 커지면 Gradient가 사라지거나 폭팔적으로 증가한다는 점이다.
예를들어 g(z) = z 라는 linear한 activation function이 있고, 아주 큰 수 L개의 레이어에 대해서 y_hat을 계산한다고 가정해보자.
y_hat 은 W^[l] W^[l-1] W^[l-2] ...W^[1] X 가 될 것이다.
만약 W의값이 1보다 작을 경우, 결국 y_hat은 급격히 감소해 0에 가까워질 것이다.
반대로 W의 값이 1보다 클 경우, 결국 y_hat은 엄청나게 커질 것이다.
이를 완전히 해결해주지는 않지만 부분적으로 해결 가능한 방법이 있다.
우리가 weight를 초기화 할 때, random initialization에 있어서 좀 더 신중하는 것이다.
예를들어 ReLU activation을 쓸때 W^[l]에다가 노드당 입력되는 특징벡터수를 나누어 곱해주는
W^[l] = np.random.rand(shape) * np.sqrt(2/n^[l-1]) 과 같은식으로 정의하면 된다.
위의 과정은 W의 편차가 2/n이 되게 해줌으로 Gradient vanishing/exploding을 줄여줄 수 있다.
Gradient Checking
f(Θ) = Θ^3 이라는 함수가 있을때
아주 작은값ϵ에 대하여 (Θ,Θ+ϵ) 에 대한 기울기를 구할때는
(f(Θ+ϵ) - f(Θ)) / ϵ 인 one sided로 구하는 것 보다
(f(Θ+ϵ) - f(Θ-ϵ)) / 2ϵ 인 two sided로 구하는 것이 오차가 더 적다.
그 이유는 테일러 급수를 통해 아래와 같이 증명할 수 있다.
따라서 앞으로 two sided method를 사용하여 Gradient checking을 하는것을 전제로 한다.
Gradient checking은 우리로 하여금 Back propagation이 올바르게 이루어지고 있는지 체크하고, 디버깅 할 수 있게 해준다.
결국 우리는 dΘ approx를 구하고, dΘ 에 대해 유클리디안 거리를 적용해서 그 값이 충분히 작으면(ex 10^-7) 올바르게 back propagation이 도입된것이라고 생각할 수 있다.
반대로 값이 크면(ex 10^-5~) 디버깅을 생각해볼 수 있다.
Gradient Checking Implementation
Gradient Checking을 실제 모델에 구현할 때에는 주의해야할 점이 몇가지 있다.
- Gradient check는 debug할때만 쓴다. Grad check를 하는 연산은 매우 느리기 때문에, 학습할때는 사용하지 않는다.
- 만약 Gradient check 결과가 이상할 경우, component들을 살펴보며 위치를 특정하면 도움이 된다.
- Regularization을 했다면 Cost function J의 식에 regularization 직을 추가하는것을 잊으면 안된다.
- Drop out이 적용된 경우에 Gradient check는 작동하지 않는다.
연관글
Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization
Practical Aspects of Deep Learning(1)