Practical Aspects of Deep Learning
- Give examples of how different types of initializations can lead to different results
- Examine the importance of initialization in complex neural networks
- Explain the difference between train/dev/test sets
- Diagnose the bias and variance issues in your model
- Assess the right time and place for using regularization methods such as dropout or L2 regularization
- Explain Vanishing and Exploding gradients and how to deal with them
- Use gradient checking to verify the accuracy of your backpropagation implementation
- Apply zeros initialization, random initialization, and He initialization
- Apply regularization to a deep learning model
Setting up Machine Learning Application
Train/Dev/Test
Train/Dev/Test data를 잘 선정하면 이는 곧 학습시간의 단축과 성능 향상으로 이어진다.
전통적으로 Machine Learning 분야에서는 Train/Test의 비율을 7:3으로, 혹은 Train/Dev/Test를 6:2:2 비율로 설정한다.
하지만 Deep Learning은 대게 대규모의 Big data 위에서 작동하기 때문에, 저렇게 까지 Dev나 Test set에 할당할 필요가 없다. 예를들어 1천만개의 Example이 있다면, Dev/Test에는 1만개만 할당해도 충분히 성능 평가가 가능할 것이다.
비율과 더불어 중요한것은 데이터의 분포이다. dev/test set는 항상 training set와 다른 종류의 데이터가 들어올 수 있다는 것을 인지해야하며, dev/test는 서로 같은 distribution에서부터 추출하여 구성하는게 좋다.
Bias / Variance
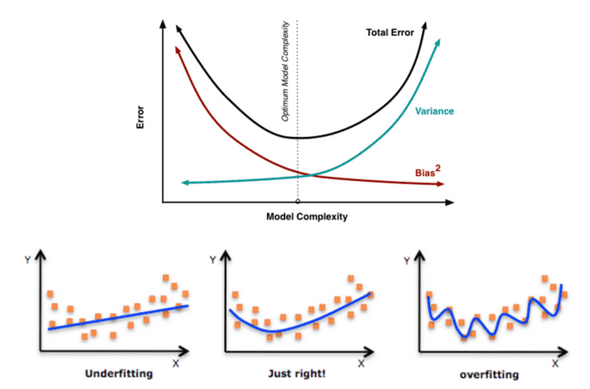
모델을 학습시키며 직면하는 문제는 Bias / Variance다.
첫번째 예시처럼 분류 결과가 underfit 하다면 high bias 상태라고 볼 수 있고
세번째 예시처럼 분류결과가 너무 overfit하다면 high variance로 볼 수 있다.
너무 overfitting 된다면 train set에 대해서는 모델의 정확도가 매우 높겠지만, test할때 조금만 다른 데이터가 들어와도 정확도가 매우 떨어지게 된다.
Underfitting은 train과 test의 정확도 차이는 별로 안나겠지만, 전체적으로 성능이 낮다.
이처럼 bias와 variance간에 trade off는 고질적인 문제인데, 다행이도 Deep learning model에서는 둘다 어느정도 해결을 할 수 있다.
만약 bias가 너무 높다면, 더욱 큰 network를 선택하거나, 더 많은 학습반복, 그리고 새로운 모델을 찾는 방법이 있을 수 있다.
variance가 너무 높다면, 더 많은 데이터를 제공해 학습을 하거나, 데이터를 Regularization하는 방법이 있다.
Regularization
Variance가 높다면 시도해볼 수 있는 방법 중 하나는 Data Regularization이다.
1.Regression
Cost functionJ(w,b)에 대해서 뒤에 특정한 값을 더해주는 것이다.
유클리디안 거리를 쓰는 L2 norm과달리 L1 norm을 사용하게 된다면 결국 w는 매우 sparse하게(0이 많게) 될것이다. 따라서 L2 norm을 쓰는게 일반적이다.
Gradient descent를 할 때에도, 원래처럼 구한 dw에 + lambda/m * w를 붙여주면 된다. (위의 식에서 앞에 1/2m 을 곱해준 이유는 미분하면 2가 상쇄되어 사라지기 때문에 일종의 트릭이다.)
그럼 최종적으로 w(1-a*lambda/m) 이되므로 w를 1보다 약간 작은수에 곱해주는 결과가 나온다.
이러한 성질때문에 L2 norm은 weight decay 라고도 불린다(참고)
그렇다면 이러한 Regularization이 overfitting을 방지하는 이유가 뭘까?
간단히 말하면, weight값을 줄여서 결과에 영향을 주는 hidden unit을 줄여 신경망이 좀더 간단하고 작은 신경망처럼 작동하게 한다.
만약 신경망이 tanh와 같은 activation function을 사용하고 있다고 할 때, regularization이 매우 커질경우 w의 값이 0과 가까운 곳에 위치하고 이는 곧 tanh함수의 linear한 부분을 의미한다. 신경망이 전체적으로 linear하게 될 경우, 앞서 봤던 overfitting처럼 복잡한 결정을 피팅하는것이 불가능해진다. 즉 선형 모델처럼 변하게 된다.
2.Drop out
또다른 강력한 Regularization 테크닉은 'Drop out' 이 있다.
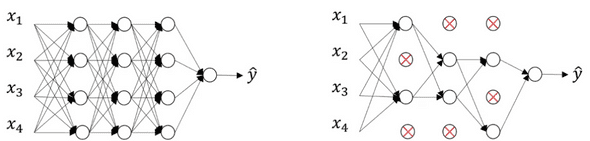
말 그대로 propagation을 할 때, 일정한 확률을 통해 랜덤하게 node들을 drop out 시킨다음 진행하는 것이다.
이렇게 학습을 1회 반복할때마다 랜덤하게 node를 drop out하는것은 매번 다른 더 작은 규모의 신경망으로 학습을 진행하는것과 같고, 이를 통해 regularization의 효과를 받는다.
예를들어 위의 그림에서 4번째 레이어의 output node는 앞의 레이어 노드들로부터 값을 전달받아 유의미한 결과를 도출해야 하는데, Drop out이 실행될 경우 매번 다른 노드로부터 입력이 들어오므로 어떤 특정한 한 노드에 의존하는 경향이 없어진다.
Drop out의 단점 중하나는 더이상 Cost function이 정확히 정의되지 않는다는 점이다. 이는 곧 Cost의 값이 내려가는 것으로 신경망이 잘 학습되고 있는지에 대한 평가 지표로 사용하지 못한다는 뜻이다.
대신 drop out 없이 신경망을 작동시켜 cost가 내려가는것을 확인하여 신경망이 올바른것을 판별하고, 다음 학습때 drop out으로 학습시키면 된다.
3.Data Augmentation
데이터의 양은 variance를 줄일 수 있는 아주 중요한 요소이다.
하지만 데이터는 경우에 따라 더이상 구할 수 없을 수도 있고, 비용이 매우 비쌀 수 도 있다.
이를 위해 우리는 이미 가지고 있는 데이터를 변형시켜 이러한 문제를 해결할 수 있다.
예를들어 이미지가 있으면, 하나의 이미지를 flip시키거나 일부분을 crop하여 데이터의 양을 늘릴 수 있다.
물론 이러한 방법이 새로운 데이터를 추가하는것 보다는 훨씬 성능이 떨어지지만, 기존의 데이터로 시간과 비용을 소모하지 않고 데이터의 양을 늘릴 수 있는 좋은 방법이다.
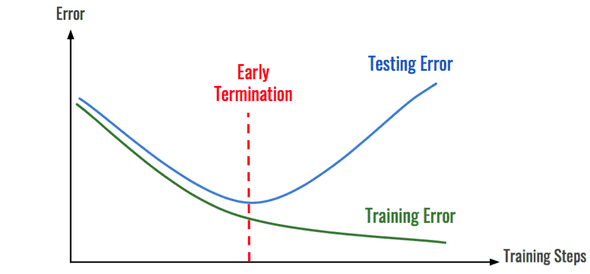
4.Early Stopping
Early Stopping은 dev/test에 대해서 cost의 값이 적당히 내려갔을때에서 학습을 멈춰 w,b의 값으로 하여금 overfitting을 막는것이다.
L2 norm과 달리 별도의 변수를 대입해가며 테스트해보지 않아도 overfitting을 막을 수 있다.
하지만 Andrew Ng은 이러한 Early stopping의 단점으로 Model을 optimizing하는것과 Overfitting을 막는것 두개의 task를 한번에 묶어버린 다는것이다.
이게 무슨 말이냐면, 원래 우리는 모델을 optimizing 하기위해 신경쓸 것은 오직 Cost function J(w,b)를 최적화하는것이다. 하지만 Early stop을 하면 J(w,b)를 최적화 하는 중간에 학습을 중단시키므로 Optimizing에 있어서 다른 방법을 더 시도해볼 수 없게된다.
연관글
Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization
Practical Aspects of Deep Learning(1)