title profile picture

PyojunCode

Reformer - Efficient Transformer

Mar 16, 2021
·

Reformer - Efficient Transformer

Original Paper : https://arxiv.org/abs/2001.04451

2021 ICLR에서 Random Feature Attention 이라는 논문이 발표되었으므로 읽어보는것도 좋다.

https://openreview.net/forum?id=QtTKTdVrFBB


Transformer Complexity

Transformer는 성능이 뛰어나지만, 연산량또한 많기 때문에 더욱 큰 모델을 만드는데 있어서 많은 도전과제들이 존재한다.

길이가 L인 sequence 를 self-Attention하려면 QK^T 를 계산하는 과정에서 L^2의 time과 memory가 필요하다.

더불어 N개의 Attention Layer를 가지고 있다면 N배의 추가적인 memory가 필요하다. Back propagation을 하기 위해 activation 값들을 저장해야 하기 때문이다.

이러한 문제를 해결하기 위해 Attention을 할 때 해당 단어와 관련이 있는 부분만을 집중적으로 보거나 activation 값을 recomputing 하는 방법들을 생각해볼 수 있다.

LSH Attention

LSH(Locality Sensitive Hashing)은 데이터의 관련도가 높으면 Hashing되는 값도 비슷하게 만드는 개념이다.

이 과정을 거치면서 비슷한 vector들로 구성된 Bucket을 구성한다.

그리고 Attention을 구하는 과정인 QK^T를 같은 Bucket 내에서만 계산을 하여 연산을 줄일 수 있다.

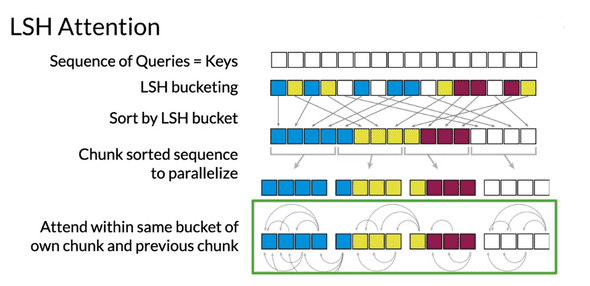
LSH를 Attention에 구체적으로 적용하는 과정은 다음과 같다.

lshatt

  • 우선 Query와 Key를 정렬한 후 LSH를 적용한다. 그 후 같은 Bucket끼리 sorting하여 정렬한다.
  • Parallelize하게 계산을 하기 위해 Bucket들을 Chunk로 나눈다. Data가 균일하지 않기 때문에 Bucket의 수도 다를 수 있으며, Chunk는 같은 수의 Bucket으로 구성되어야 한다.
  • 나누어진 Chunk안의 bucket들끼리, 혹은 앞 chunk의 같은 bucket에 대하여 Attention을 진행한다.

따라서 각 Data가 최대 자신과 앞의 chunk에 대해서만 attention하므로 전체 attention 횟수는 l * (2l/c)^2 이다. chunk의 개수 c가 충분히 크다면 l^2에 비해 훨씬 개선된 성능을 낼 수 있다.

Reversible Layers

만약 책 한권 전체에 대해서 Transformer를 사용하고 싶다면 수백만개의 토큰이 발생할 수 있다.

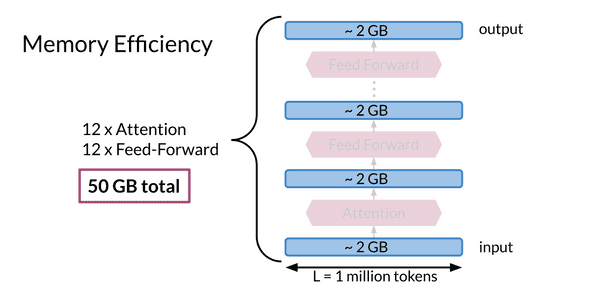
만약 d_model 즉 embedding depth가 512만 되도 이미 Input data만으로도 2GB를 차지한다.

mem

이러한 상황에서 12개의 Attention과 Feed Forward Layer를 가지고 있는 Transformer model에 해당 데이터를 학습시키면 이미 필요한 메모리는 50GB를 초과한다. 이는 매우 비효율적인 메모리 사용이고, 한개의 GPU로는 감당할 수 없을 것이다.

이런 Residual Layer의 구조를 가지고 있는 기존의 모델은 결과에서 역으로 원래 입력값을 계산해내지 못하기 때문에 계속 memory에 값을 allocate하고 있어야하는 문제가 있다.

따라서 이 문제를 해결하기 위해 새로운 layer 구조를 생각해볼 수 있다.

reversible

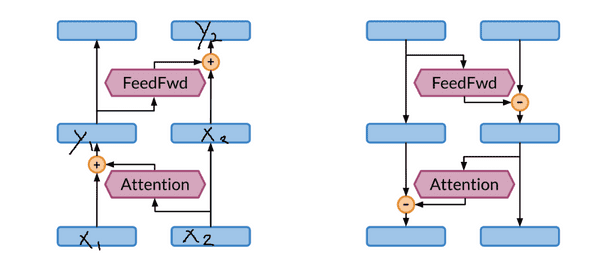
처음의 Input을 두개로 복사하여 위와 같은 Layer 구조를 거치면, 기존과 다르게 역으로 계산이 가능하다.

reveq

두 Input 중 Attention이나 Feed Forward를 거치지 않는 쪽은 Residual하게 더해주는데에 사용된다. 뿐 만 아니라 역으로 계산할 때 x1,x2이 서로 Dependency 를 갖지 않으므로 따로 메모리에 저장할 필요 없이 계산이 가능하다.

(Dropout 같은 layer는 noise가 있기 때문에, forward와 backward에서 random으로 생성되는값이 다를 경우 값이 일치하지 않게된다. 따라서 seed를 정하던가 해서 일치시켜주어야함.)

Implement in Trax

Reversible layer

def reversible_layer_forward(x, f, g):
    """
    Args: 
        x (np.array): an input vector or matrix
        f (function): a function which operates on a vector/matrix
        g (function): a function which operates on a vector/matrix
    Returns: 
        y (np.array): an output vector or matrix whose form is determined by 'x', f and g
    """
    # split or duplicate
    x1, x2 = np.split(x, 2, axis=-1) 
    
    y1 = x1 + f(x2)
    
    y2 = x2 + g(y1) 
    
    y = np.concatenate((y1,y2),axis=-1)
    
    return y
def reversible_layer_reverse(y, f, g):
    """
    Args: 
        y (np.array): an input vector or matrix
        f (function): a function which operates on a vector/matrix of the form of 'y'
        g (function): a function which operates on a vector/matrix of the form of 'y'
    Returns: 
        y (np.array): an output vector or matrix whose form is determined by 'y', f and g
    """
    
    # split
    y1, y2 = np.split(y, 2, axis=-1)
    
    x2 = y2 - g(y1)

    x1 = y1-f(x2)

    x = np.concatenate((x1,x2),axis=-1)
    
    return x