Dynamic Programming(DP)

Dynamic Programming이란 어떠한 문제가 sub problems들로 나누어질 수 있고, 중복되는(overlapping) sub problems의 답을 쌓아가며 활용해 원래 problem의 답에 도달하게 만드는 기법이다.

큰 문제를 여러개의 sub problems으로 나눈다는 것에서 앞서 배운 quick sort나 merge sort같은 devide and conquer문제와 유사한 것 같지만, sub problem에서 도출되는 답이 다른 sub problem에도 중복되어 쓰이지(overlapping) 않으므로 DP라고 할 수 없다.

결국 Dynamic Programming을 쓰기 위한 조건은 두 가지가 있는데,

• 문제의 답을 sub problem으로 나누고 합쳐서 도출해낼 수 있는가. (optimal structure)
• sub problems들이 overlapping(겹침)되는가

위의 조건을 만족하면 DP로 풀 수 있다.

빠른 이해를 위해 간단한 예제를 생각해보면 피보나치 수열을 예로 들 수 있다.

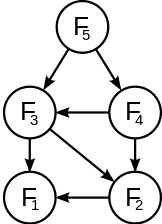
피보나치 수열에서 F(n) = F(n-1)+F(n-2)이다 만약 F(5)를 구한다고 하면,

아래와 같이 sub problem 트리를 나타낼 수 있다.

만약 dp를 사용하지 않고 해당 문제를 푼다고 한다면 F(3)을 구하기위해 F(2),F(1)을 계산할 것이고 F(4)를 구하기 위해 F(3),F(2)를 계산해야 할 것이다. 즉, F(2)를 두번 계산하여 비효율적이다.

이 때 F(2)가 위에서 설명한 overlapping sub problems의 예라고 볼 수 있다.

따라서 이 값을 매번 구하는게 아니라 answer table에 저장하는 memoize 하면서 효율있게 DP로 답을 구할 수 있다.

1. 각  sub problem의 답을 저장할 table을 정의.
2. 문제를 해결할 수 있는 점화식 찾기.
3. 초기값 정의

DP에서 제일 중요한건 바로 2번 점화식 찾기라고 할 수 있다. 어떠한 점화식을 세워야 초기의 값 몇개만으로도 원하는 답에 도달할 수 있는지를 잘 생각해야한다.

마치며

DP는 어떤 문제를 보고 DP로 풀어야겠다고 생각할 수 있는 통찰력을 키우는게 중요하다. 따라서 시간날 때 마다 DP문제를 많이 풀어보면 좋다.